
分析 (1)把a=1代入函数解析式,再由f(x)≥log23结合对数函数的单调性化为一元二次不等式求解;
(2)由题意可得ax2-3ax+5>0对任意x∈R恒成立,然后对a分类求解得答案.
解答 解:(1)a=1时,
$f(x)=lo{g}_{2}({x}^{2}-3x+5)$,
则f(x)≥log23?$lo{g}_{2}({x}^{2}-3x+5)≥lo{g}_{2}3$,
即x2-3x+5≥3,解得x≤1或x≥2.
∴不等式f(x)≥log23的解集为(-∞,1]∪[2,+∞);
(2)∵f(x)的定义域为R,
∴ax2-3ax+5>0对任意x∈R恒成立,
当a>0时,△=9a2-20a<0,解得$0<a<\frac{20}{9}$.
又a=0成立,
∴a的取值范围是[0,$\frac{20}{9}$).
点评 本题考查对数不等式的解法,考查分类讨论的数学思想方法与数学转化思想方法,是中档题.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
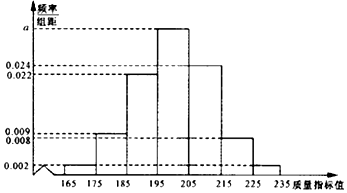 某食品公司研发生产一种新的零售食品,从产品中抽取100件作为样本,测量这些产品的一项质量指标值,由测量结果得到如图频率分布直方图.
某食品公司研发生产一种新的零售食品,从产品中抽取100件作为样本,测量这些产品的一项质量指标值,由测量结果得到如图频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | $[{\frac{1}{2},2}]$ | C. | (0,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com