
���� �������⣬���|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=$\sqrt{3}$����$\overrightarrow{a}$��$\overrightarrow{b}$�ļн�Ϊ$\frac{��}{3}$ʱ$\overrightarrow{a}$•$\overrightarrow{b}$ȡ�����ֵ��|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=3����$\overrightarrow{a}$��$\overrightarrow{b}$�ļн�Ϊ$\frac{2��}{3}$ʱ$\overrightarrow{a}$•$\overrightarrow{b}$ȡ����Сֵ��
��� �⣺ƽ������$\overrightarrow{a}$��$\overrightarrow{b}$����|$\overrightarrow{a}$|��|$\overrightarrow{b}$|��|$\overrightarrow{a}$+$\overrightarrow{b}$|��[1��3]��
��${��\overrightarrow{a}+\overrightarrow{b}��}^{2}$=${\overrightarrow{a}}^{2}$+2$\overrightarrow{a}$•$\overrightarrow{b}$+${\overrightarrow{b}}^{2}$��[1��9]��
��$\overrightarrow{a}$•$\overrightarrow{b}$��[$\frac{1}{2}$-$\frac{{\overrightarrow{a}}^{2}{+\overrightarrow{b}}^{2}}{2}$��$\frac{9}{2}$-$\frac{{\overrightarrow{a}}^{2}{+\overrightarrow{b}}^{2}}{2}$]��
��|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=$\sqrt{3}$����$\overrightarrow{a}$��$\overrightarrow{b}$�ļн�Ϊ$\frac{��}{3}$ʱ��|$\overrightarrow{a}$+$\overrightarrow{b}$|=3��
��ʱ$\overrightarrow{a}$•$\overrightarrow{b}$=$\sqrt{3}$��$\sqrt{3}$��cos$\frac{��}{3}$=$\frac{3}{2}$��ȡ�����ֵ��
��|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=3����$\overrightarrow{a}$��$\overrightarrow{b}$�ļн�Ϊ$\frac{2��}{3}$ʱ��|$\overrightarrow{a}$+$\overrightarrow{b}$|=3��
��ʱ$\overrightarrow{a}$•$\overrightarrow{b}$=3��3��cos$\frac{2��}{3}$=-$\frac{9}{2}$��ȡ����Сֵ��
��$\overrightarrow{a}$•$\overrightarrow{b}$��ȡֵ��Χ��[-$\frac{9}{2}$��$\frac{3}{2}$]��
�ʴ�Ϊ��[-$\frac{9}{2}$��$\frac{3}{2}$]��
���� ���⿼����ƽ�������������Ķ�����Ӧ�����⣬���ۺ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 0 | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
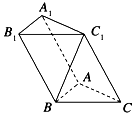 ��ͼ����б������ABC-A1B1C1�У���BAC=90�㣬BC1��AC����PΪ������A1B1C1
��ͼ����б������ABC-A1B1C1�У���BAC=90�㣬BC1��AC����PΪ������A1B1C1| A�� | ��ABC���ڲ� | B�� | ��ABC���ⲿ | C�� | ֱ��AB�� | D�� | ���Ͼ��п��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com