练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．若α为锐角，sinα-mcosα=a（m＞0），则msinα+cosα=$\sqrt{{m}^{2}+1{-a}^{2}}$．

    分析 根据（sinα-mcosα）2=a2，（msinα+cosα）2+（sinα-mcosα）2=m2+1，可得msinα+cosα的值．

    解答 解：∵α为锐角sinα-mcosα=a，（m＞0），∴（sinα-mcosα）2=a2，
    又  （msinα+cosα）2+（sinα-mcosα）2=m2+1，∴（msinα+cosα）2=m2+1-a2，
    ∴msinα+cosα=$\sqrt{{m}^{2}+1{-a}^{2}}$，
    故答案为：$\sqrt{{m}^{2}+1{-a}^{2}}$．

    点评 本题主要考查同角三角函数的基本关系的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    2．如图所示的程序框图，运行程序后，输出的结果为（　　）
    A．5B．4C．3D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知一几何体的三视图如图所示，则该几何体的表面积为（　　）
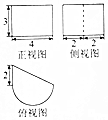
    A．14+6$\sqrt{5}$+10πB．14+6$\sqrt{5}$+20πC．12+12πD．26+6$\sqrt{5}$+10π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．高考结束后高三的8名同学准备拼车去旅游，其中一班、二班、三班、四班每班各两名，分乘甲、乙两辆汽车，每车限坐4名同学（乘同一辆车的4名同学不考虑位置，）其中一班两位同学是孪生姐妹，需乘同一辆车，则乘坐甲车的4名同学中恰有2名同学是来自同一班的乘坐方式共有（　　）
    A．18种B．24种C．48种D．36种

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．甲、乙两家外卖公司，其送餐员的日工资方案如下：甲公司的底薪70元，每单抽成4元；乙公司无底薪，40单以内（含40单）的部分每单抽成5元，超出40单的部分每单抽成7元，假设同一公司送餐员一天的送餐单数相同，现从两家公司各随机抽取一名送餐员，并分别记录其100天的送餐单数，得到如表频数表：
    甲公司送餐员送餐单数频数表
     送餐单数 38 39 40 41 42
     天数 20 40 20 10 10
    乙公司送餐员送餐单数频数表
     送餐单数 38 39 40 41 42
     天数 10 20 20 40 10
    （Ⅰ）现从甲公司记录的100天中随机抽取两天，求这两天送餐单数都大于40的概率；
    （Ⅱ）若将频率视为概率，回答下列问题：
    （i）记乙公司送餐员日工资为X（单位：元），求X的分布列和数学期望；
    （ii）小明拟到甲、乙两家公司中的一家应聘送餐员，如果仅从日工资的角度考虑，请利用所学的统计学知识为他作出选择，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知P（0，1）是椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）上一点，点P到椭圆C的两个焦点的距离之和为2$\sqrt{2}$．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）设A，B是椭圆C上异于点P的两点，直线PA与直线x=4交于点M，是否存在点A，使得S△ABP=$\frac{1}{2}{S_{△ABM}}$？若存在，求出点A的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．下列说法错误的是（　　）
    A．命题，“若x2-3x+2=0，则x=1”的逆否命题为：“若x≠1，则x2-3x+2≠0“
    B．对于命题p：?x0∈R，x02+x0+1＜0，则￢p：?x∈R，x2+x+1≥0
    C．若m，n∈R，“lnm＜lnn“是“em＜en”的必要不充分条件
    D．若p∨q为假命题，则p，q均为假命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|，|$\overrightarrow{b}$|，|$\overrightarrow{a}$+$\overrightarrow{b}$|∈[1，3]．则$\overrightarrow{a}$•$\overrightarrow{b}$的取值范围是[-$\frac{9}{2}$，$\frac{3}{2}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

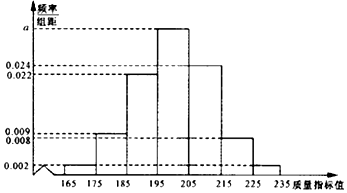    13．某食品公司研发生产一种新的零售食品，从产品中抽取100件作为样本，测量这些产品的一项质量指标值，由测量结果得到如图频率分布直方图．
    （Ⅰ）求直方图中a的值；
    （Ⅱ）由频率分布直方图可以认为，这种产品的质量指标值Z服从正态分布N（200，12.22），试计算数据落在（187.8，212.2）上的频率；
    参考数据
    若Z～N（μ，δ2），则P（μ-δ＜Z＜μ+δ）=0.6826，P（μ-2δ＜Z＜μ+2δ）=0.9544．
    （Ⅲ）设生产成本为y，质量指标为x，生产成本与质量指标之间满足函数关系y=$\left\{\begin{array}{l}{0.4x，x≤205}\\{0.8x-80，x＞205}\end{array}\right.$，假设同组中的每个数据用该组区间的右端点值代替，试计算生产该食品的平均成本．

    查看答案和解析>>

    同步练习册答案