练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．高考结束后高三的8名同学准备拼车去旅游，其中一班、二班、三班、四班每班各两名，分乘甲、乙两辆汽车，每车限坐4名同学（乘同一辆车的4名同学不考虑位置，）其中一班两位同学是孪生姐妹，需乘同一辆车，则乘坐甲车的4名同学中恰有2名同学是来自同一班的乘坐方式共有（　　）
    A．18种B．24种C．48种D．36种

    分析 分类讨论，第一类，一班的2名同学在甲车上；第二类，一班的2名同学不在甲车上，再利用组合知识，问题得以解决．

    解答 解：由题意，第一类，一班的2名同学在甲车上，甲车上剩下两个要来自不同的班级，从三个班级中选两个为C32=3，然后分别从选择的班级中再选择一个学生为C21C21=4，故有3×4=12种．
    第二类，一班的2名同学不在甲车上，则从剩下的3个班级中选择一个班级的两名同学在甲车上，为C31=3，然后再从剩下的两个班级中分别选择一人为C21C21=4，这时共有3×4=12种，
    根据分类计数原理得，共有12+12=24种不同的乘车方式，
    故选：B．

    点评 本题考查计数原理的应用，考查组合知识，考查学生的计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    10．已知x，y满足约束条件$\left\{{\begin{array}{l}{x-y+2≥0}\\{x+2y-2≥0}\\{x≤2}\end{array}}\right.$，则目标函数z=-x+2y的最大值为6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知函数f（x）=ax3-3x2+1，若f（-a）、f（a）、f（3a）成公差不为0的等差数列，则过坐标原点作曲线y=f（x）的切线可以作（　　）
    A．0条B．1条C．2条D．3条

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知向量$\overrightarrow{a}$=（sinθ，1），$\overrightarrow{b}$=（-sinθ，0），$\overrightarrow{c}$=（cosθ，-1），且（2$\overrightarrow{a}$-$\overrightarrow{b}$）∥$\overrightarrow{c}$，则tanθ等于-$\frac{2}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知函数f（x）=|x+1|-|x-3|．
    （Ⅰ）画出函数f（x）的图象；
    （Ⅱ）若不等式f（x）≥$\frac{|3m+1|-|1-m|}{|m+1|}$对任意实数m≠-1，求实数x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知f（x）=x3-3x+2+m（m＞0），在区间[0，2]上存在三个不同的实数a，b，c，使得以f（a），f（b），f（c）为边长的三角形是直角三角形，则m的取值范围是0＜m＜4+4$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．若α为锐角，sinα-mcosα=a（m＞0），则msinα+cosα=$\sqrt{{m}^{2}+1{-a}^{2}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．在等腰梯形ABCD中，已知AB∥DC，AB=2CD=4．若$\overrightarrow{AC}$•$\overrightarrow{BD}$=-1，则$\overrightarrow{AD}$•$\overrightarrow{BC}$=7．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

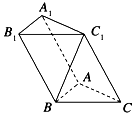    1．如图，在斜三棱柱ABC-A1B1C1中，∠BAC=90°，BC1⊥AC，若P为三角形A1B1C1
    内一点（不含边界），则点P在底面ABC的投影可能在（　　）
    A．△ABC的内部B．△ABC的外部C．直线AB上D．以上均有可能

    查看答案和解析>>

    同步练习册答案