练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．已知向量$\overrightarrow{a}$=（sinθ，1），$\overrightarrow{b}$=（-sinθ，0），$\overrightarrow{c}$=（cosθ，-1），且（2$\overrightarrow{a}$-$\overrightarrow{b}$）∥$\overrightarrow{c}$，则tanθ等于-$\frac{2}{3}$．

    分析 2$\overrightarrow{a}$-$\overrightarrow{b}$=（3sinθ，2），利用向量共线定理即可得出．

    解答 解：2$\overrightarrow{a}$-$\overrightarrow{b}$=（3sinθ，2），
    ∵（2$\overrightarrow{a}$-$\overrightarrow{b}$）∥$\overrightarrow{c}$，∴-3sinθ-2cosθ=0，
    解得tanθ=-$\frac{2}{3}$．
    故答案为：-$\frac{2}{3}$．

    点评 本题考查了向量共线定理、三角函数求值，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    18．已知复数z1=1-i，z2=-2+3i，则复数$\frac{{i•{z_2}}}{z_1}$对应的点在（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

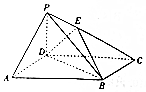    19．如图所示，在四棱锥P-ABCD中，底面ABCD为平行四边形，∠DBA=30°，$\sqrt{3}$AB=2BD，PD=AD，PD⊥底面ABCD，E为PC上一点，且PE=$\frac{1}{2}$EC．
    （1）证明：PA⊥BD；
    （2）若AD=$\sqrt{6}$，求三棱锥E-CBD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．在平面直角坐标系xOy中，双曲线E：$\frac{{x}^{2}}{{a}^{2}}$-y2=1（a＞0）的左右焦点分别为F1、F2，离心率为$\frac{2\sqrt{3}}{3}$，且经过右焦点F2的直线l与双曲线的右支交于A、B两点．
    （1）求双曲线E的方程；
    （2）求△ABF1的面积的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知一几何体的三视图如图所示，则该几何体的表面积为（　　）
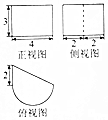
    A．14+6$\sqrt{5}$+10πB．14+6$\sqrt{5}$+20πC．12+12πD．26+6$\sqrt{5}$+10π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=xlnx+a（a∈R），g（x）=$\frac{2x}{{e}^{x-1}}$-e（e为自然对数的底数）．
    （Ⅰ）讨论函数f（x）的零点个数；
    （Ⅱ）求证：当x＞0时，f（x）＞g（x）+a．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．高考结束后高三的8名同学准备拼车去旅游，其中一班、二班、三班、四班每班各两名，分乘甲、乙两辆汽车，每车限坐4名同学（乘同一辆车的4名同学不考虑位置，）其中一班两位同学是孪生姐妹，需乘同一辆车，则乘坐甲车的4名同学中恰有2名同学是来自同一班的乘坐方式共有（　　）
    A．18种B．24种C．48种D．36种

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知P（0，1）是椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）上一点，点P到椭圆C的两个焦点的距离之和为2$\sqrt{2}$．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）设A，B是椭圆C上异于点P的两点，直线PA与直线x=4交于点M，是否存在点A，使得S△ABP=$\frac{1}{2}{S_{△ABM}}$？若存在，求出点A的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知命题p：?x0∈R，使2${\;}^{{x}_{0}}$+2${\;}^{-{x}_{0}}$=1；命题q：?x∈R，都有lg（x2+2x+3）＞0．下列结论中正确的是（　　）
    A．命题“￢p∧q”是真命题B．命题“p∧￢q”是真命题
    C．命题“p∧q”是真命题D．命题“￢p∨￢q”是假命题

    查看答案和解析>>

    同步练习册答案