练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
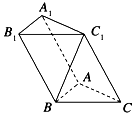
    1．如图，在斜三棱柱ABC-A1B1C1中，∠BAC=90°，BC1⊥AC，若P为三角形A1B1C1
    内一点（不含边界），则点P在底面ABC的投影可能在（　　）
    A．△ABC的内部B．△ABC的外部C．直线AB上D．以上均有可能

    分析 由题意结合线面垂直的判定可得平面ABC1⊥平面ABC，再由线面垂直的性质可得C1在底面ABC的射影H的位置，即可得出结论．

    解答 解：∵AC⊥AB，AC⊥BC1，
    ∴AC⊥平面ABC1，AC?平面ABC，
    ∴平面ABC1⊥平面ABC，
    ∴C1在平面ABC上的射影H必在两平面的交线AB上．
    若P为三角形A1B1C1
    内一点（不含边界），则点P在底面ABC的投影可能在△ABC的外部，
    故选：B．

    点评 本题考查棱柱的结构特征，考查了线面垂直的判定和性质，考查空间想象能力，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    20．高考结束后高三的8名同学准备拼车去旅游，其中一班、二班、三班、四班每班各两名，分乘甲、乙两辆汽车，每车限坐4名同学（乘同一辆车的4名同学不考虑位置，）其中一班两位同学是孪生姐妹，需乘同一辆车，则乘坐甲车的4名同学中恰有2名同学是来自同一班的乘坐方式共有（　　）
    A．18种B．24种C．48种D．36种

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|，|$\overrightarrow{b}$|，|$\overrightarrow{a}$+$\overrightarrow{b}$|∈[1，3]．则$\overrightarrow{a}$•$\overrightarrow{b}$的取值范围是[-$\frac{9}{2}$，$\frac{3}{2}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知命题p：?x0∈R，使2${\;}^{{x}_{0}}$+2${\;}^{-{x}_{0}}$=1；命题q：?x∈R，都有lg（x2+2x+3）＞0．下列结论中正确的是（　　）
    A．命题“￢p∧q”是真命题B．命题“p∧￢q”是真命题
    C．命题“p∧q”是真命题D．命题“￢p∨￢q”是假命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

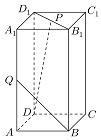    16．如图，设长方体ABCD-A1B1C1D1中，AB=BC=1，AA1=2，Q是AA1的中点，点P在线段B1D1上；
    （1）试在线段B1D1上确定点P的位置，使得异面直线QB与DP所成角为60°，并请说明
    你的理由；
    （2）在满足（1）的条件下，求四棱锥Q-DBB1P的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．在二项式${（{x^2}-\frac{1}{x}）^5}$的展开式中，含x4项的系数是a，则${∫}_{1}^{a}$x-1dx=10．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

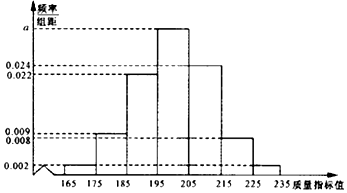    13．某食品公司研发生产一种新的零售食品，从产品中抽取100件作为样本，测量这些产品的一项质量指标值，由测量结果得到如图频率分布直方图．
    （Ⅰ）求直方图中a的值；
    （Ⅱ）由频率分布直方图可以认为，这种产品的质量指标值Z服从正态分布N（200，12.22），试计算数据落在（187.8，212.2）上的频率；
    参考数据
    若Z～N（μ，δ2），则P（μ-δ＜Z＜μ+δ）=0.6826，P（μ-2δ＜Z＜μ+2δ）=0.9544．
    （Ⅲ）设生产成本为y，质量指标为x，生产成本与质量指标之间满足函数关系y=$\left\{\begin{array}{l}{0.4x，x≤205}\\{0.8x-80，x＞205}\end{array}\right.$，假设同组中的每个数据用该组区间的右端点值代替，试计算生产该食品的平均成本．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点A（0，3），与双曲线$\frac{{x}^{2}}{14}-\frac{{y}^{2}}{13}$=1有相同的焦点
    （1）求椭圆C的方程；
    （2）过A点作两条相互垂直的直线，分别交椭圆C于P，Q两点，则PQ是否过定点？若是，求出定点的坐标，若不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．我国古代数学专著《孙子算法》中有“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？”如果此物数量在100至200之间，那么这个数128．

    查看答案和解析>>

    同步练习册答案