
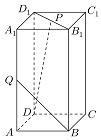
 如图,设长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,Q是AA1的中点,点P在线段B1D1上;
如图,设长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,Q是AA1的中点,点P在线段B1D1上;分析 (1)以D为坐标原点,分别以DA、DC、DD1所在直线为x、y、z轴建立空间直角坐标系,设D1P=λD1B1,把P的坐标用λ表示,然后分别求出$\overrightarrow{DP}、\overrightarrow{QB}$的坐标,再由|cos<$\overrightarrow{DP},\overrightarrow{QB}$>|=cos60°列式求得λ值得答案;
(2)由图可得四棱锥Q-DBB1P的高为A1P,再求出底面直角梯形的面积,代入棱锥体积公式求得四棱锥Q-DBB1P的体积.
解答 解:(1)P是线段B1D1中点.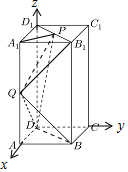
证明如下:
以D为坐标原点,分别以DA、DC、DD1所在直线为x、y、z轴建立空间直角坐标系,
则D(0,0,0),Q(1,0,1),B(1,1,0),D1(0,0,2),B1(1,1,2),
设D1P=λD1B1,则$\overrightarrow{{D}_{1}P}=(λ,λ,0)$,∴P(λ,λ,2),
∴$\overrightarrow{DP}$=(λ,λ,2),又$\overrightarrow{QB}$=(0,1,-1),
∴|cos<$\overrightarrow{DP},\overrightarrow{QB}$>|=|$\frac{\overrightarrow{DP}•\overrightarrow{QB}}{|\overrightarrow{DP}||\overrightarrow{QB}|}$|=cos60$°=\frac{1}{2}$.
∴|$\frac{λ-2}{\sqrt{2{λ}^{2}+4}×\sqrt{2}}$|=$\frac{1}{2}$,解得:$λ=\frac{1}{2}$;
(2)连接A1P,则A1P⊥平面DBB1D1,
∵A1Q∥平面DBB1D1,∴四棱锥Q-DBB1P的高为${A}_{1}P=\frac{\sqrt{2}}{2}$.
${S}_{四边形DB{B}_{1}P}=\frac{1}{2}×(\sqrt{2}+\frac{\sqrt{2}}{2})×2$=$\frac{3\sqrt{2}}{2}$.
∴${V}_{Q-DB{B}_{1}P}=\frac{1}{3}×\frac{3\sqrt{2}}{2}×\frac{\sqrt{2}}{2}$=$\frac{1}{2}$.
点评 本题考查利用空间向量求解异面直线所成角,考查了棱锥体积的求法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 已知函数f(x)=|x+1|-|x-3|.
已知函数f(x)=|x+1|-|x-3|.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -$\frac{4}{5}$ | C. | $\frac{4}{5}$ | D. | ±$\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
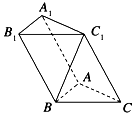 如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,若P为三角形A1B1C1
如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,若P为三角形A1B1C1| A. | △ABC的内部 | B. | △ABC的外部 | C. | 直线AB上 | D. | 以上均有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{4}{3}$ | B. | ±$\frac{3}{4}$ | C. | ±$\frac{3}{5}$ | D. | ±$\frac{5}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com