
分析 求出f(x)的解析式,判断f(x)的单调性,利用f(x)的单调性得出f(x)的最大值.
解答 解:解不等式$\left\{\begin{array}{l}{4x+1≤x+2}\\{4x+1≤-2x+4}\end{array}\right.$得:x$≤\frac{1}{3}$;
解不等式$\left\{\begin{array}{l}{x+2≤4x+1}\\{x+2≤-2x+4}\end{array}\right.$得:$\frac{1}{3}$≤x≤$\frac{2}{3}$,
解不等式$\left\{\begin{array}{l}{-2x+4≤4x+1}\\{-2x+4≤x+2}\end{array}\right.$得:x$≥\frac{2}{3}$,
∴f(x)=$\left\{\begin{array}{l}{4x+1,x≤\frac{1}{3}}\\{x+2,\frac{1}{3}<x<\frac{2}{3}}\\{-2x+4,x≥\frac{2}{3}}\end{array}\right.$,
∴f(x)在(-∞,$\frac{1}{3}$]上单调递增,在($\frac{1}{3}$,$\frac{2}{3}$)上单调递增,在[$\frac{2}{3}$,+∞)上单调递减,
∴当x=$\frac{2}{3}$时,f(x)取得最大值f($\frac{2}{3}$)=$\frac{8}{3}$.
故答案为$\frac{8}{3}$.
点评 本题考查了不等式的解法,函数单调性的判断及最值计算,属于中档题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:选择题
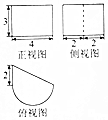
| A. | 14+6$\sqrt{5}$+10π | B. | 14+6$\sqrt{5}$+20π | C. | 12+12π | D. | 26+6$\sqrt{5}$+10π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题,“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0“ | |
| B. | 对于命题p:?x0∈R,x02+x0+1<0,则¬p:?x∈R,x2+x+1≥0 | |
| C. | 若m,n∈R,“lnm<lnn“是“em<en”的必要不充分条件 | |
| D. | 若p∨q为假命题,则p,q均为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“¬p∧q”是真命题 | B. | 命题“p∧¬q”是真命题 | ||
| C. | 命题“p∧q”是真命题 | D. | 命题“¬p∨¬q”是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
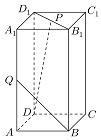 如图,设长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,Q是AA1的中点,点P在线段B1D1上;
如图,设长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,Q是AA1的中点,点P在线段B1D1上;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
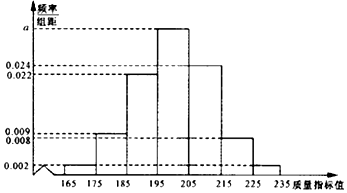 某食品公司研发生产一种新的零售食品,从产品中抽取100件作为样本,测量这些产品的一项质量指标值,由测量结果得到如图频率分布直方图.
某食品公司研发生产一种新的零售食品,从产品中抽取100件作为样本,测量这些产品的一项质量指标值,由测量结果得到如图频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com