
分析 令f(x)=t,借助函数图象判断方程f(x)=t的解的情况,从而得出关于t的方程t2+bt+c=0在(0,+∞)上根的分布情况,进而求出x1,x2,x3.
解答 解:作出y=f(x)的函数图象如图所示: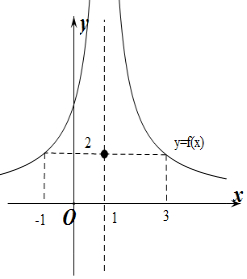
令f(x)=t,
由图象可知当且仅当t=2时,方程f(x)=t有3解;
当0<t<2或t>2时,方程f(x)=t有两解;
当t≤0时,方程f(x)=t无解.
∵关于x的方程f2(x)+bf(x)+c=0有三个不同的实数解,
∴关于t的方程t2+bt+c=0在(0,+∞)上只有一解t=2.
令f(x)=2得x1=-1,x2=1,x3=3.
∴${x_1}^2+{x_2}^2+{x_3}^2$=(-1)2+12+32=11.
故答案为:11.
点评 本题考查了函数零点与函数图象的关系,属于中档题.


科目:高中数学 来源: 题型:解答题
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 20 | 40 | 20 | 10 | 10 |
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 10 | 20 | 20 | 40 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
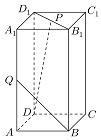 如图,设长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,Q是AA1的中点,点P在线段B1D1上;
如图,设长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,Q是AA1的中点,点P在线段B1D1上;查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
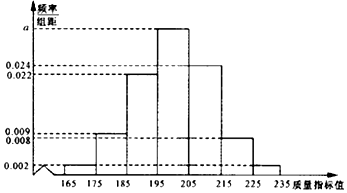 某食品公司研发生产一种新的零售食品,从产品中抽取100件作为样本,测量这些产品的一项质量指标值,由测量结果得到如图频率分布直方图.
某食品公司研发生产一种新的零售食品,从产品中抽取100件作为样本,测量这些产品的一项质量指标值,由测量结果得到如图频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | $[{\frac{1}{2},2}]$ | C. | (0,2] | D. | [2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com