
分析 根据“三三数之剩二,五五数之剩三,七七数之剩二”找到三个数:第一个数能同时被3和5整除;第二个数能同时被3和7整除;第三个数能同时被5和7整除,将这三个数分别乘以被7、5、3除的余数再相加即可求出答案.
解答 解:我们首先需要先求出三个数:
第一个数能同时被3和5整除,但除以7余1,即15;
第二个数能同时被3和7整除,但除以5余1,即21;
第三个数能同时被5和7整除,但除以3余1,即70;
然后将这三个数分别乘以被7、5、3除的余数再相加,即:15×2+21×3+70×2=233.
最后,再减去3、5、7最小公倍数的整数倍,可得:233-105×2=23.或105k+23(k为正整数).
由于物数量在100至200之间,故当k=1时,105+23=128
故答案为:128
点评 本题考查的是带余数的除法,简单的合情推理的应用,根据题意下求出15、21、70这三个数是解答此题的关键.[可以原文理解为:三个三个的数余二,七个七个的数也余二,那么,总数可能是三乘七加二,等于二十三.二十三用五去除余数又恰好是三]


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案科目:高中数学 来源: 题型:选择题
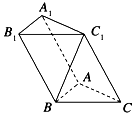 如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,若P为三角形A1B1C1
如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,若P为三角形A1B1C1| A. | △ABC的内部 | B. | △ABC的外部 | C. | 直线AB上 | D. | 以上均有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2<x<2} | B. | {x|-2<x<3} | C. | {x|-1<x<3} | D. | {x|-1<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
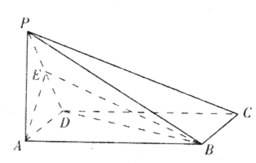 如图,四棱锥P-ABCD的底面ABCD为矩形,PA⊥底面ABCD,AD=AP=2,AB=2$\sqrt{7}$,E为棱PD的中点.
如图,四棱锥P-ABCD的底面ABCD为矩形,PA⊥底面ABCD,AD=AP=2,AB=2$\sqrt{7}$,E为棱PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 微信群数量(个) | 频数 | 频率 |
| 0~4 | 0.15 | |
| 5~8 | 40 | 0.4 |
| 9~12 | 25 | |
| 13~16 | a | c |
| 16以上 | 5 | b |
| 合计 | 100 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com