
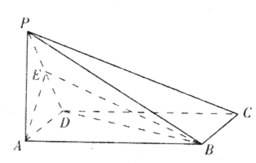
 如图,四棱锥P-ABCD的底面ABCD为矩形,PA⊥底面ABCD,AD=AP=2,AB=2$\sqrt{7}$,E为棱PD的中点.
如图,四棱锥P-ABCD的底面ABCD为矩形,PA⊥底面ABCD,AD=AP=2,AB=2$\sqrt{7}$,E为棱PD的中点.分析 (Ⅰ)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法能证明PD⊥平面ABE.
(Ⅱ)三棱锥C-PBD外接球即以AB,AD,AP为棱的长方体的外接球,由此能求出三棱锥C-PBD外接球的体积.
解答 证明:(Ⅰ)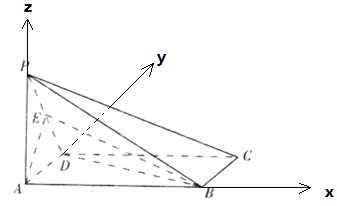 以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
P(0,0,2),D(0,2,0),A(0,0,0),B(2$\sqrt{7}$,0,0),E(0,1,1),
$\overrightarrow{PD}$=(0,2,-2),$\overrightarrow{AB}$=(2$\sqrt{7}$,0,0),$\overrightarrow{AE}$=(0,1,1),
$\overrightarrow{PD}$$•\overrightarrow{AB}$=0,$\overrightarrow{PD}•\overrightarrow{AE}$=0,
∴PD⊥AB,PD⊥AE,
∵AB∩AE=A,∴PD⊥平面ABE.
解:(Ⅱ)∵AD,AP,AB两垂直,底面ABCD为矩形,
∴三棱锥C-PBD外接球即以AB,AD,AP为棱的长方体的外接球,
∴三棱锥C-PBD外接球的半径R=$\frac{\sqrt{4+4+28}}{2}$=3,
∴三棱锥C-PBD外接球的体积V=$\frac{4}{3}π{R}^{3}$=$\frac{4}{3}π×27$=36π.
点评 本题考查线面垂直的证明,考查三棱锥的外接的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
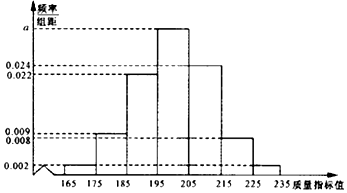 某食品公司研发生产一种新的零售食品,从产品中抽取100件作为样本,测量这些产品的一项质量指标值,由测量结果得到如图频率分布直方图.
某食品公司研发生产一种新的零售食品,从产品中抽取100件作为样本,测量这些产品的一项质量指标值,由测量结果得到如图频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 156里 | B. | 84里 | C. | 66里 | D. | 42里 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
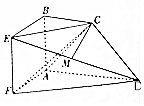 如图,已知四边形ABEF于ABCD分别为正方形和直角梯形,平面ABEF⊥平面ABCD,AB=BC=$\frac{1}{2}$AD=1,AB⊥AD,BC∥AD,点M是棱ED的中点.
如图,已知四边形ABEF于ABCD分别为正方形和直角梯形,平面ABEF⊥平面ABCD,AB=BC=$\frac{1}{2}$AD=1,AB⊥AD,BC∥AD,点M是棱ED的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com