
| A�� | 156�� | B�� | 84�� | C�� | 66�� | D�� | 42�� |
���� ������ɵã�����ÿ�����ߵ�·�γɵȱ�����{an}������q=$\frac{1}{2}$��S6=378�����õȱ����е�ͨ�ʽ�����ʽ���ɵó���
��� �⣺������ɵã�����ÿ�����ߵ�·�γɵȱ�����{an}������q=$\frac{1}{2}$��S6=378��
��$\frac{{a}_{1}[1-��\frac{1}{2}��^{6}]}{1-\frac{1}{2}}$=378�����a1=192��
��3��һ������a4+a5+a6=${a}_{1}��{q}^{3}+{q}^{4}+{q}^{5}��$=192��$��\frac{1}{2}��^{3}$��$[1+\frac{1}{2}+��\frac{1}{2}��^{2}]$=42��
��ѡ��D��
���� ���⿼���˵ȱ����е�ͨ�ʽ�����ʽ��������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
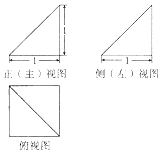
| A�� | 4�� | B�� | 3�� | C�� | 12�� | D�� | 8�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|-2��x��2} | B�� | {x|-2��x��3} | C�� | {x|-1��x��3} | D�� | {x|-1��x��2} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
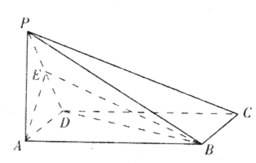 ��ͼ������P-ABCD�ĵ���ABCDΪ���Σ�PA�͵���ABCD��AD=AP=2��AB=2$\sqrt{7}$��EΪ��PD���е㣮
��ͼ������P-ABCD�ĵ���ABCDΪ���Σ�PA�͵���ABCD��AD=AP=2��AB=2$\sqrt{7}$��EΪ��PD���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��Ⱥ���������� | Ƶ�� | Ƶ�� |
| 0��4 | 0.15 | |
| 5��8 | 40 | 0.4 |
| 9��12 | 25 | |
| 13��16 | a | c |
| 16���� | 5 | b |
| �ϼ� | 100 | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|1��x��3} | B�� | {x|-1��x��3} | C�� | {x|-1��x��0��0��x��3} | D�� | {x|-1��x��0��1��x��3} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com