分析:(1)欲证A1C⊥B1C1,即证线面垂直,为了要证明线面垂直,即要证线线垂直,其中利用勾股定理证明AC⊥BC即可;
(2)利用空间向量的坐标法求解,先建立空间直角坐标系,设点的坐标,利用点B1到平面A1BC的距离公式求解;
(3)先求出平面A1BC1的一个法向量,再利用两个向量的夹角公式求解二面角C1-A1B-C的大小即可.
解答: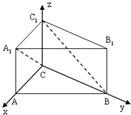
证明:(1)在△ABC中,BC
2=16+4-2×4×2×cos60
0=12,(2分)
∵AB
2=AC
2+BC
2,
∴AC⊥BC,
∵A
1A⊥平面ABC,
∴A
1C⊥BC,
∵B
1C
1∥BC,
∴A
1C⊥B
1C
1.(4分)
(2)由(1)知,AC⊥BC.建立如图直角坐标系,
则A
1(2,0,2),
B(0 , 2 , 0)B1(0 , 2 , 2)易求得,平面A
1BC的一个法向量
=(1 , 0 , -1),
∴点B
1到平面A
1BC的距离
d==.(8分)
(3)可求得平面A
1BC
1的一个法向量
=(0 , 1 , ),
cos<,>==-,
∴二面角C
1-A
1B-C的大小是
arccos.(12分)
点评:本题主要考查了平面与平面之间的位置关系,以及空间中直线与直线之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.

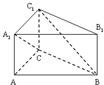 如图,直三棱柱ABC-A1B1C1中,AB=4,AC=AA1=2,∠BAC=60°.
如图,直三棱柱ABC-A1B1C1中,AB=4,AC=AA1=2,∠BAC=60°. 证明:(1)在△ABC中,BC2=16+4-2×4×2×cos600=12,(2分)
证明:(1)在△ABC中,BC2=16+4-2×4×2×cos600=12,(2分)

 如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB=
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB= 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点. 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.