
(12分)化简(1)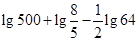
(2)已知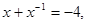 求
求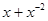 的值。
的值。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
某车间有50名工人,要完成150件产品的生产任务,每件产品由3个A 型零件和1个B 型零件配套组成.每个工人每小时能加工5个A 型零件或者3个B 型零件,现在把这些工人分成两组同时工作(分组后人数不再进行调整),每组加工同一中型号的零件.设加工A 型零件的工人人数为x名(x∈N*)
(1)设完成A 型零件加工所需时间为 小时,写出
小时,写出 的解析式;
的解析式;
(2)为了在最短时间内完成全部生产任务,x应取何值?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设二次函数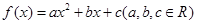 满足下列条件:
满足下列条件:
①当 时,
时,  的最小值为0,且
的最小值为0,且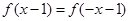 恒成立;
恒成立;
②当 时,
时,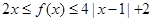 恒成立.
恒成立.
(I)求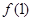 的值;
的值;
(Ⅱ)求 的解析式;
的解析式;
(Ⅲ)求最大的实数m(m>1),使得存在实数t,只要当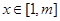 时,就有
时,就有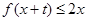 成立
成立
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知定义在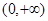 的函数
的函数 ,对任意的
,对任意的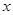 、
、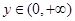 ,都有
,都有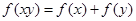 ,且当
,且当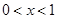 时,
时,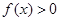 .
.
(1)证明:当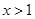 时,
时,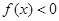 ;
;
(2)判断函数 的单调性并加以证明;
的单调性并加以证明;
(3)如果对任意的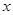 、
、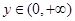 ,
,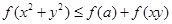 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某公园计划建造一个室内面积为800m2的矩形花卉温室.在温室内,沿左、右两侧与后侧内墙各保留1m宽的通道。沿前侧内墙保留3m宽的空地,中间矩形内种植花卉.当矩形温室的边长各为多少时,花卉的种植面积最大?最大种植面积是多少?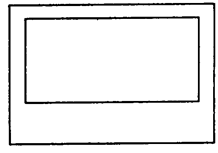
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题共12分)
已知函数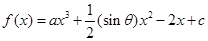 的图象过点
的图象过点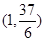 ,且在
,且在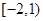 内单调递减,在
内单调递减,在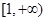 上单调递增。
上单调递增。
(1)求 的解析式;
的解析式;
(2)若对于任意的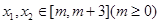 ,不等式
,不等式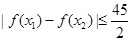 恒成立,试问这样的
恒成立,试问这样的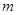 是否存在.若存在,请求出
是否存在.若存在,请求出 的范围,若不存在,说明理由;
的范围,若不存在,说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了绿化城市,准备在如图所示的区域内修建一个矩形PQRC的草坪,且PQ//BC,RQ BC。另外
BC。另外 的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?
的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
本小题满分12分)
今有一长2米宽1米的矩形铁皮,如图,在四个角上分别截去一个边长为x米的正方形后,沿虚线折起可做成一个无盖的长方体形水箱(接口连接问题不考虑).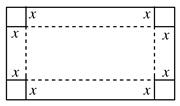
(Ⅰ)求水箱容积的表达式 ,并指出函数
,并指出函数 的定义域;
的定义域;
(Ⅱ)若要使水箱容积不大于 立方米的同时,又使得底面积最大,求x的值.
立方米的同时,又使得底面积最大,求x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有一批运动服装原价为每套80元,两个商场均有销售,为了吸引顾客,两商场纷纷推出优惠政策。甲商场的优惠办法是:买一套减4元,买两套每套减8元,买三套每套减12元,......,依此类推,直到减到半价为止;乙商场的优惠办法是:一律7折。某单位欲为每位员工买一套运动服装,问选择哪个商场购买更省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com