
为了绿化城市,准备在如图所示的区域内修建一个矩形PQRC的草坪,且PQ//BC,RQ BC。另外
BC。另外 的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?
的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
某地西红柿上市时间仅能持续5个月,预测上市初期和后期会因供不应求使价格呈连续上涨势态,而中期又将出现供大于求使价格连续下跌。现有三种价格模拟函数:① ,②
,②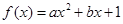 ,③
,③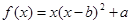 ,(以上三式中
,(以上三式中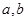 均是不为零的常数,且
均是不为零的常数,且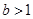 )
)
(1) 为了准确研究其价格走势,应选择哪种价格模拟函数,为什么?
(2)若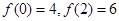 ,求出所选函数
,求出所选函数 的解析式(注:函数的定义域是
的解析式(注:函数的定义域是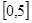 )。其中
)。其中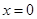 表示8月1日,
表示8月1日,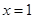 表示9月1日,……,以此类推;为保证该地的经济收益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该西红柿将在哪几个月份内价格下跌。
表示9月1日,……,以此类推;为保证该地的经济收益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该西红柿将在哪几个月份内价格下跌。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题共8分)
提高二环路的车辆通行能力可有效改善整个城区的交通状况,在一般情况下,二环路上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数。当二环路上的车流密度达到600辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过60辆/千米时,车流速度为80千米/小时,研究表明:当60≤x≤600时,车流速度v是车流密度x的一次函数。
(Ⅰ)当0≤x≤600时,求函数f(x)的表达式;
(Ⅱ)当车流密度x为多大时,车流量(单位时间内通过二环路上某观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值。(精确到1辆/小时)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
一次函数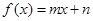 与指数型函数
与指数型函数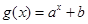 ,(
,(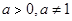 )的图像交于两点
)的图像交于两点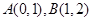 ,解答下列各题
,解答下列各题 :
:
(1)求一次函数 和指数型函数
和指数型函数 的表达式;
的表达式;
(2)作出这两个函数的图像;
(3)填空:当 时,
时,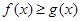 ;当
;当 时,
时,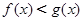 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com