
(本小题满分12分).已知幂函数 的图象关于
的图象关于 轴对称,且在区间
轴对称,且在区间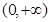 上是减函数,
上是减函数,
(1)求函数 的解析式;((2)若
的解析式;((2)若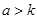 ,比较
,比较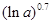 与
与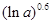 的大小;
的大小;
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
一艘轮船在航行过程中的燃料费与它的速度的立方成正比例关系,其他与速度无关的费用每小时96元,已知在速度为每小时10公里时,每小时的燃料费是6元,要使行驶1公里所需的费用总和最小,这艘轮船的速度应确定为每小时多少公里?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设二次函数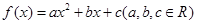 满足下列条件:
满足下列条件:
①当 时,
时,  的最小值为0,且
的最小值为0,且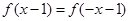 恒成立;
恒成立;
②当 时,
时,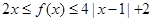 恒成立.
恒成立.
(I)求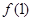 的值;
的值;
(Ⅱ)求 的解析式;
的解析式;
(Ⅲ)求最大的实数m(m>1),使得存在实数t,只要当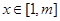 时,就有
时,就有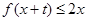 成立
成立
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商家有一种商品,成本费为a 元,如果月初售出可获利100元,再将本利都存入银行,已知银行月息为2.4%,如果月末售出可获利120元,但要付保管费5元,试就 a的取值说明这种商品是月初售出好,还是月末售出好?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知定义在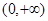 的函数
的函数 ,对任意的
,对任意的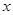 、
、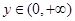 ,都有
,都有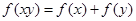 ,且当
,且当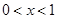 时,
时,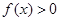 .
.
(1)证明:当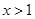 时,
时,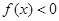 ;
;
(2)判断函数 的单调性并加以证明;
的单调性并加以证明;
(3)如果对任意的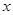 、
、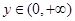 ,
,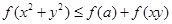 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某公园计划建造一个室内面积为800m2的矩形花卉温室.在温室内,沿左、右两侧与后侧内墙各保留1m宽的通道。沿前侧内墙保留3m宽的空地,中间矩形内种植花卉.当矩形温室的边长各为多少时,花卉的种植面积最大?最大种植面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了绿化城市,准备在如图所示的区域内修建一个矩形PQRC的草坪,且PQ//BC,RQ BC。另外
BC。另外 的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?
的内部有一文物保护区不能占用,经测量AB="100m," BC="80m," AE="30m," AF=20m,应如何设计才能使草坪的占地面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)已知某公司生产某品牌服装的年固定成本为10万元,每生产一千件,需要另投入2.7万元.设该公司年内共生产该品牌服装 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为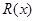 万元,且
万元,且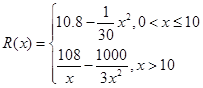 .
.
(I)写出年利润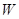 (万元)关于年产量
(万元)关于年产量 (千件)的函数关系式;
(千件)的函数关系式;
(Ⅱ)年生产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
建造一间占 地面积为12m²的背面靠墙的猪圈,底面为长方形,猪圈正面的造价为每平方米12元,侧面的造价为每平方米80元,屋顶造价为1120元.如果墙高3m,且不计猪圈背面的费用,问:如何设计能使猪圈的总 造价最低?最低总造价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com