
设二次函数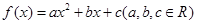 满足下列条件:
满足下列条件:
①当 时,
时,  的最小值为0,且
的最小值为0,且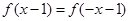 恒成立;
恒成立;
②当 时,
时,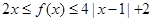 恒成立.
恒成立.
(I)求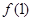 的值;
的值;
(Ⅱ)求 的解析式;
的解析式;
(Ⅲ)求最大的实数m(m>1),使得存在实数t,只要当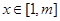 时,就有
时,就有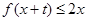 成立
成立
(1) f(1)="2" ;(2) f(x)= 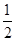 (x+1)2; (3) m的最大值为9.
(x+1)2; (3) m的最大值为9.
解析试题分析:(1)在②中令x=1,有2≤f(1)≤2,故f(1)="2"
(2)由①知二次函数的关于直线x=-1对称,且开口向上
故设此二次函数为f(x)=a(x+1)2,(a>0),∵f(1)=2,∴a=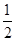
∴f(x)= 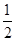 (x+1)2
(x+1)2
(3)假设存在t∈R,只需x∈[1,m],就有f(x+t)≤2x.
f(x+t)≤2x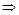
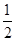 (x+t+1)2≤2x
(x+t+1)2≤2x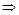 x2+(2t-2)x+t2+2t+1≤0.
x2+(2t-2)x+t2+2t+1≤0.
令g(x)=x2+(2t-2)x+t2+2t+1,g(x)≤0,x∈[1,m].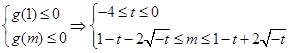
∴m≤1-t+2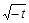 ≤1-(-4)+2
≤1-(-4)+2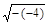 =9
=9
t=-4时,对任意的x∈[1,9]
恒有g(x)≤0, ∴m的最大值为9.(画图用数形结合视解答情况给分)
考点:本题主要考查二次函数的图象和性质,简单不等式组的解法。
点评:典型题,本题综合考查“二次问题”,运用了从特殊到一般的思想方法。(3)作为存在性问题,转化成一个二次不等式在给定闭区间恒成立问题,借助于函数单调性,通过限制区间端点函数值的范围,得到不等式组,使问题得解。


科目:高中数学 来源: 题型:解答题
已知:在函数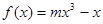 的图象上,以
的图象上,以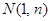 为切点的切线的倾斜角为
为切点的切线的倾斜角为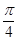 .
.
(Ⅰ)求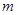 ,
, 的值;
的值;
(Ⅱ)是否存在最小的正整数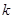 ,使得不等式
,使得不等式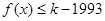 对于
对于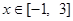 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数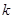 ;如果不存在,请说明理由;
;如果不存在,请说明理由;
(Ⅲ)求证: (
(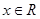 ,
,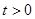 ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地西红柿上市时间仅能持续5个月,预测上市初期和后期会因供不应求使价格呈连续上涨势态,而中期又将出现供大于求使价格连续下跌。现有三种价格模拟函数:① ,②
,②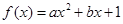 ,③
,③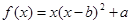 ,(以上三式中
,(以上三式中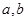 均是不为零的常数,且
均是不为零的常数,且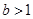 )
)
(1) 为了准确研究其价格走势,应选择哪种价格模拟函数,为什么?
(2)若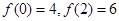 ,求出所选函数
,求出所选函数 的解析式(注:函数的定义域是
的解析式(注:函数的定义域是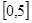 )。其中
)。其中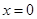 表示8月1日,
表示8月1日,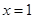 表示9月1日,……,以此类推;为保证该地的经济收益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该西红柿将在哪几个月份内价格下跌。
表示9月1日,……,以此类推;为保证该地的经济收益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该西红柿将在哪几个月份内价格下跌。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售高订购,决定当一次订量超过100个时,每多订购一个,订购的全部零件的出厂单价降低0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少个时,零件的实际出厂单价恰好降为51元?
(2)设一次订购量为x个,零件的实际出厂单价为P元,写出函数P=f(x)的表达式.
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1 000个,利润又是多少元(工厂售出一个零件的利润=实际出厂单价-成本价)?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
一次函数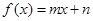 与指数型函数
与指数型函数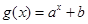 ,(
,(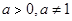 )的图像交于两点
)的图像交于两点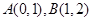 ,解答下列各题
,解答下列各题 :
:
(1)求一次函数 和指数型函数
和指数型函数 的表达式;
的表达式;
(2)作出这两个函数的图像;
(3)填空:当 时,
时,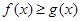 ;当
;当 时,
时,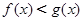 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com