
如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?
广告的高为140 cm,宽为175 cm时,可使广告的面积最小
解析试题分析:解法1:设矩形栏目的高为a cm,宽为b cm,则ab=9000. ①
广告的高为a+20,宽为2b+25,其中a>0,b>0.
广告的面积S=(a+20)(2b+25)
=2ab+40b+25a+500=18500+25a+40b
≥18500+2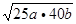 =18500+
=18500+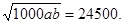
当且仅当25a=40b时等号成立,此时b=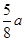 ,代入①式得a=120,从而b=75.
,代入①式得a=120,从而b=75.
即当a=120,b=75时,S取得最小值24500.
故广告的高为140 cm,宽为175 cm时,可使广告的面积最小.
解法2:设广告的高为宽分别为x cm,y cm,则每栏的高和宽分别为x-20,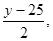 其中x>20,y>25
其中x>20,y>25
两栏面积之和为2(x-20)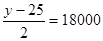 ,由此得y=
,由此得y=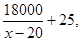
广告的面积S=xy=x(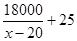 )=
)=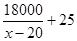 x,
x,
整理得S=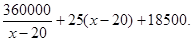
因为x-20>0,所以S≥2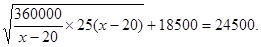
当且仅当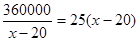 时等号成立,
时等号成立,
此时有(x-20)2=14400(x>20),解得x=140,代入y=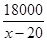 +25,得y=175,
+25,得y=175,
即当x=140,y=175时,S取得最小值24500,
故当广告的高为140 cm,宽为175 cm时,可使广告的面积最小.
考点:不等式求解最值
点评:解决的关键是利用函数的性质或者是均值不等式求解最值,关键是设好变量,表示广告的面积,属于基础题。


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:解答题
某公司试销一种新产品,规定试销时销售单价不低于成本单价500元/件,又不高于800元/件,经试销调查,发现销售量y(件)与销售单价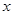 (元/件),可近似看做一次函数
(元/件),可近似看做一次函数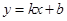 的关系(图象如下图所示).
的关系(图象如下图所示).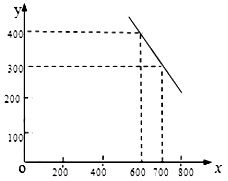
(1)根据图象,求一次函数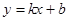 的表达式;
的表达式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元,
①求S关于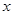 的函数表达式;
的函数表达式;
②求该公司可获得的最大毛利润,并求出此时相应的销售单价.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
己知某公司生产某品牌服装的年固定成木为10万元,每生产一千件需另投入2.7万元,设该公司年内共生产该品牌服装x千件并全部销售完,每销售一千件的收入为R(x)万元,且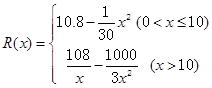
(注:年利润=年销售收入一年总成本)
(1)写出年利润W(万元)关于年产品x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设二次函数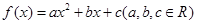 满足下列条件:
满足下列条件:
①当 时,
时,  的最小值为0,且
的最小值为0,且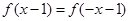 恒成立;
恒成立;
②当 时,
时,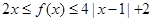 恒成立.
恒成立.
(I)求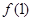 的值;
的值;
(Ⅱ)求 的解析式;
的解析式;
(Ⅲ)求最大的实数m(m>1),使得存在实数t,只要当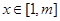 时,就有
时,就有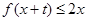 成立
成立
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知定义在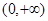 的函数
的函数 ,对任意的
,对任意的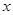 、
、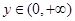 ,都有
,都有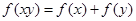 ,且当
,且当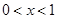 时,
时,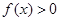 .
.
(1)证明:当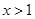 时,
时,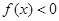 ;
;
(2)判断函数 的单调性并加以证明;
的单调性并加以证明;
(3)如果对任意的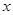 、
、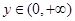 ,
,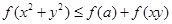 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题共12分)
已知函数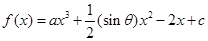 的图象过点
的图象过点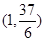 ,且在
,且在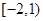 内单调递减,在
内单调递减,在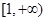 上单调递增。
上单调递增。
(1)求 的解析式;
的解析式;
(2)若对于任意的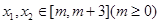 ,不等式
,不等式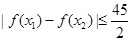 恒成立,试问这样的
恒成立,试问这样的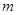 是否存在.若存在,请求出
是否存在.若存在,请求出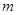 的范围,若不存在,说明理由;
的范围,若不存在,说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com