
化简求值:(12分)
(1) (2)
(2)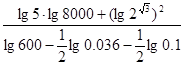
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
提高大桥的车辆通行能力可改善整个城市的交通状况.一般情况下,大桥上的车流
速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当车流密度不超过50辆/千米时,车流速度为30千米/小时.研究表明:当50<x≤200时,车流速度v与车流密度x满足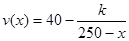 .当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时.
.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时.
(Ⅰ)当0<x≤200时,求函数v(x)的表达式;
(Ⅱ)当车流密度x为多大时,车流量(单位时间内通过桥上观测点的车辆数,单位:
辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到个位,参考数据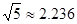 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分15分)
经过长期的观测得到:在交通繁忙时段,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(千米/小时)之间的函数关系为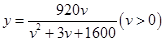 .
.
(1)在该时段内,当汽车的平均速度v为多少时,车流量最大?最大车流量为多少?
(精确到0.1千辆/小时)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
已知二次函数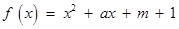 ,关于
,关于 的不等式
的不等式 的解集为
的解集为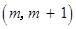 ,其中
,其中 为非零常数.设
为非零常数.设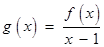 .
.
(1)求 的值;
的值;
(2)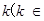 R
R 如何取值时,函数
如何取值时,函数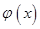
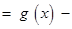
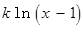 存在极值点,并求出极值点;
存在极值点,并求出极值点;
(3)若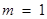 ,且
,且
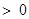 ,求证:
,求证: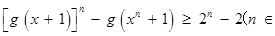 N
N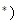
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
图1是某种称为“凹槽”的机械部件的示意图,图2是凹槽的横截面(阴影部分)示意图,其中四边形ABCD是矩形,弧CmD是半圆,凹槽的横截面的周长为4.已知凹槽的强度与横截面的面积成正比,比例系数为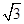 ,设AB=2x,BC=y.
,设AB=2x,BC=y.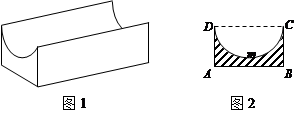
(1)写出y关于x函数表达式,并指出x的取值范围;
(2)求当x取何值时,凹槽的强度最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com