
【题目】已知椭圆C: ![]() =1(a>b>0),离心率为
=1(a>b>0),离心率为 ![]() ,左准线方程是x=﹣2,设O为原点,点A在椭圆C上,点B在直线y=2上,且OA⊥OB.
,左准线方程是x=﹣2,设O为原点,点A在椭圆C上,点B在直线y=2上,且OA⊥OB. 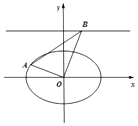
(1)求椭圆C的方程;
(2)求△AOB面积取得最小值时,线段AB的长度.
【答案】
(1)解:设椭圆的半焦距为c,则离心率e= ![]() =
= ![]() ,准线方程:x=﹣
,准线方程:x=﹣ ![]() =2,
=2,
解得:c=1,a= ![]() ,
,
由b2=a2﹣c2=1,
椭圆C的方程: ![]()
(2)解:由题意,直线OA的斜率存在,设直线OA的斜率为k,
若k=0时,则A( ![]() ,0)或(﹣
,0)或(﹣ ![]() ,0),B(0,2),
,0),B(0,2),
此时△AOB面积为 ![]() ,AB=
,AB= ![]() .
.
若k≠0时,则直线OA:y=kx,A(x1,y1),B(x2,y2),
将y=kx代入椭圆 ![]() ,整理得:(1+2k2)x2﹣2=0,
,整理得:(1+2k2)x2﹣2=0,
由韦达定理可知:可得丨OA丨= ![]()
![]() =
= ![]()
![]() ,
,
直线OB:y=﹣ ![]() x与y=2联立得:B(﹣2k,2),则OB=2
x与y=2联立得:B(﹣2k,2),则OB=2 ![]() ,
,
S△OAB= ![]() OAOB=
OAOB= ![]()
![]() ,
,
令t= ![]() >1,
>1,
则S△OAB= ![]()
![]() =
= ![]() (t+
(t+ ![]() )>
)> ![]() ,
,
∴S△OAB的最小值为 ![]() ,在k=0时取得,此时AB=
,在k=0时取得,此时AB= ![]()
【解析】(1)由题意可得:e= ![]() =
= ![]() ,x=﹣
,x=﹣ ![]() =2,联立求得a和c的值,由b2=a2﹣c2 , 即可求得b的值,求得椭圆方程;(2)当k=0时,则A(
=2,联立求得a和c的值,由b2=a2﹣c2 , 即可求得b的值,求得椭圆方程;(2)当k=0时,则A( ![]() ,0)或(﹣
,0)或(﹣ ![]() ,0),B(0,2),此时△AOB面积为
,0),B(0,2),此时△AOB面积为 ![]() ,AB=
,AB= ![]() ,当k≠0时,设直线OA方程,代入椭圆方程,利用韦达定理,弦长公式及三角形的面积公式,根据基本不等式的性质求得△AOB面积取得最小值,即可求得k的值,求得线段AB的长度.
,当k≠0时,设直线OA方程,代入椭圆方程,利用韦达定理,弦长公式及三角形的面积公式,根据基本不等式的性质求得△AOB面积取得最小值,即可求得k的值,求得线段AB的长度.


科目:高中数学 来源: 题型:
【题目】连续抛掷同一颗均匀的骰子,令第i次得到的点数为ai , 若存在正整数k,使a1+a2+…+ak=6,则称k为你的幸运数字.
(1)求你的幸运数字为3的概率;
(2)若k=1,则你的得分为5分;若k=2,则你的得分为3分;若k=3,则你的得分为1分;若抛掷三次还没找到你的幸运数字则记0分,求得分X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
(1)设AD=x(x≥1),ED=y,求用x表示y的函数关系式;
(2)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请予证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() =1(a>b>0)的左、右焦点分别为F1,F2,P是椭圆上一点,|PF1|=λ|PF2|
=1(a>b>0)的左、右焦点分别为F1,F2,P是椭圆上一点,|PF1|=λ|PF2|![]() ,∠F1PF2=
,∠F1PF2=![]() ,则椭圆离心率的取值范围为( )
,则椭圆离心率的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:x﹣y=1与圆M:x2+y2﹣2x+2y﹣1=0相交于A,C两点,点B,D分别在圆M上运动,且位于直线AC两侧,则四边形ABCD面积的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于两个定义域均为D的函数f(x),g(x),若存在最小正实数M,使得对于任意x∈D,都有|f(x)﹣g(x)|≤M,则称M为函数f(x),g(x)的“差距”,并记作||f(x),g(x)||.
(1)求f(x)=sinx(x∈R),g(x)=cosx(x∈R)的差距;
(2)设f(x)= ![]() (x∈[1,e
(x∈[1,e ![]() ]),g(x)=mlnx(x∈[1,e
]),g(x)=mlnx(x∈[1,e ![]() ]).(e≈2.718)
]).(e≈2.718)
①若m=2,且||f(x),g(x)||=1,求满足条件的最大正整数a;
②若a=2,且||f(x),g(x)||=2,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设常数a≥0,函数f(x)=x﹣ln2x+2alnx﹣1
(1)令g(x)=xf'(x)(x>0),求g(x)的最小值,并比较g(x)的最小值与0的大小;
(2)求证:f(x)在(0,+∞)上是增函数;
(3)求证:当x>1时,恒有x>ln2x﹣2alnx+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解甲、乙两个工厂生产的轮胎的宽度是否达标,分别从两厂随机各选取了![]() 个轮胎,将每个轮胎的宽度(单位:
个轮胎,将每个轮胎的宽度(单位: ![]() )记录下来并绘制出如下的折线图:
)记录下来并绘制出如下的折线图:
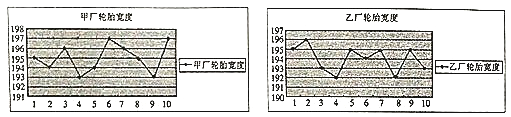
(1)分别计算甲、乙两厂提供的![]() 个轮胎宽度的平均值;
个轮胎宽度的平均值;
(2)轮胎的宽度在![]() 内,则称这个轮胎是标准轮胎.
内,则称这个轮胎是标准轮胎.
(i)若从甲乙提供的![]() 个轮胎中随机选取
个轮胎中随机选取![]() 个,求所选的轮胎是标准轮胎的概率
个,求所选的轮胎是标准轮胎的概率![]() ;
;
(ii)试比较甲、乙两厂分别提供的![]() 个轮胎中所有标准轮胎宽度的方差大小,根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个厂的轮胎相对更好?
个轮胎中所有标准轮胎宽度的方差大小,根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个厂的轮胎相对更好?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com