
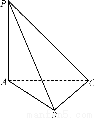
如图,在三棱锥P-ABC中,△PAC,△ABC分别是以A、B为直角顶点的等腰直角三角形,AB=1.现给出三个条件:①PB=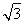 ;②PB⊥BC;③平面PAB⊥平面ABC.试从中任意选取一个作为已知条件,并证明:PA⊥平面ABC;
;②PB⊥BC;③平面PAB⊥平面ABC.试从中任意选取一个作为已知条件,并证明:PA⊥平面ABC;
见解析
【解析】(解法1)选取条件①,在等腰直角三角形ABC中,∵AB=1,∴BC=1,AC=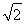 .
.
又∵PA=AC,∴PA=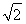 .∴在△PAB中,AB=1,PA=
.∴在△PAB中,AB=1,PA=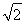 .
.
又∵PB=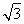 ,∴AB2+PA2=PB2.∴∠PAB=90°,即PA⊥AB.
,∴AB2+PA2=PB2.∴∠PAB=90°,即PA⊥AB.
又∵PA⊥AC,AB∩AC=A,AB,AC真包含于平面ABC,∴PA⊥平面ABC.
(解法2)选取条件②,
∵PB⊥BC,又AB⊥BC,且PB∩AB=B,∴BC⊥平面PAB.
∵PA真包含于平面PAB,∴BC⊥PA.
又∵PA⊥AC,且BC∩AC=C,∴PA⊥平面ABC.
(解法3)选取条件③,
若平面PAB⊥平面ABC,
∵平面PAB∩平面ABC=AB,BC真包含于平面ABC,BC⊥AB,∴BC⊥平面PAB.
∵PA真包含于平面PAB,∴BC⊥PA.∵PA⊥AC,且BC∩AC=C,∴PA⊥平面ABC.


科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第六章第1课时练习卷(解析版) 题型:解答题
已知f(x)=-3x2+a(6-a)x+b.
(1)解关于a的不等式f(1)>0;
(2)当不等式f(x)>0的解集为(-1,3)时,求实数a、b的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第5课时练习卷(解析版) 题型:解答题
如图①所示,在Rt△ABC中,AC=6,BC=3,∠ABC=90°,CD为∠ACB的平分线,点E在线段AC上,CE=4.如图②所示,将△BCD沿CD折起,使得平面BCD⊥平面ACD,连结AB,设点F是AB的中点.
 图①
图① 图②
图②
(1)求证:DE⊥平面BCD;
(2)若EF∥平面BDG,其中G为直线AC与平面BDG的交点,求三棱锥B-DEG的体积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第4课时练习卷(解析版) 题型:解答题
如图①,E、F分别是直角三角形ABC边AB和AC的中点,∠B=90°,沿EF将三角形ABC折成如图②所示的锐二面角A1EFB,若M为线段A1C的中点.求证:
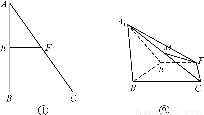
(1)直线FM∥平面A1EB;
(2)平面A1FC⊥平面A1BC.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第4课时练习卷(解析版) 题型:填空题
a、b、c为三条不重合的直线,α、β、γ为三个不重合平面,现给出六个命题:
①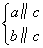 a∥b;②
a∥b;②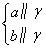 a∥b;③
a∥b;③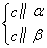 α∥β;
α∥β;
④ α∥β;⑤
α∥β;⑤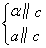 α∥a;⑥
α∥a;⑥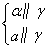 a∥α.
a∥α.
其中正确的命题是________.(填序号)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第3课时练习卷(解析版) 题型:填空题
如图所示,b,c在平面α内,a∩c=B,b∩c=A,且a⊥b,a⊥c,b⊥c,若C∈a,D∈b,E在线段AB上(C、D、E均异于A、B),则△ACD的形状是________.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第3课时练习卷(解析版) 题型:解答题
如图,在正三棱柱ABCA1B1C1中,A1A= AC,D、E、F分别为线段AC、A1A、C1B的中点.
AC,D、E、F分别为线段AC、A1A、C1B的中点.

(1)证明:EF∥平面ABC;
(2)证明:C1E⊥平面BDE.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第2课时练习卷(解析版) 题型:解答题
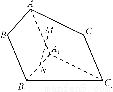
如图所示,在三棱柱ABCA1B1C1中,M、N分别是BC和A1B1的中点.求证:MN∥平面AA1C1.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(解析版) 题型:填空题
根据市场调查结果,预测某种家用商品从年初开始的n个月内累积的需求量Sn(万件)近似地满足关系式Sn=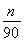 (21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________.
(21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com