
【题目】经过多年的运作,“双十一”抢购活动已经演变成为整个电商行业的大型集体促销盛宴.为迎接2014年“双十一”网购狂欢节,某厂家拟投入适当的广告费,对网上所售产品进行促销.经调查测算,该促销产品在“双十一”的销售量p万件与促销费用x万元满足![]() (其中
(其中![]() ,a为正常数).已知生产该产品还需投入成本
,a为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为
![]() 元/件,假定厂家的生产能力完全能满足市场的销售需求.
元/件,假定厂家的生产能力完全能满足市场的销售需求.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大?
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若![]() 是函数
是函数![]() 的一个极值点,试求
的一个极值点,试求![]() 的单调区间;
的单调区间;
(2)若![]() 且
且![]() ,是否存在实数a,使得
,是否存在实数a,使得![]() 在区间
在区间![]() 上的最大值为4?若存在,求出实数a的值;若不存在,请说明理由.
上的最大值为4?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)设椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 、
、![]() ,
,![]() 是椭圆
是椭圆![]() 与双曲线
与双曲线![]() 的公共点,且△
的公共点,且△![]() 的周长为6,求椭圆
的周长为6,求椭圆![]() 的方程;我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”;
的方程;我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”;
(2)如图,已知“盾圆![]() ”的方程为
”的方程为![]() ,设“盾圆
,设“盾圆![]() ”上的任意一点
”上的任意一点![]() 到
到![]() 的距离为
的距离为![]() ,
,![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)由抛物线弧![]() (
(![]() )与第(1)小题椭圆弧
)与第(1)小题椭圆弧![]()
![]() (
(![]() )所合成的封闭曲线为“盾圆
)所合成的封闭曲线为“盾圆![]() ”,设过点
”,设过点![]() 的直线与“盾圆
的直线与“盾圆![]() ”交于
”交于![]() 、
、![]() 两点,
两点,![]() ,
,![]() ,且
,且![]() (
(![]() ),试用
),试用![]() 表示
表示![]() ,并求
,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,其中
,其中![]() .
.
(1)若![]() ,写出
,写出![]() 的单调区间:
的单调区间:
(2)若函数![]() 恰有三个不同的零点,且这些零点之和为-2,求a、b的值;
恰有三个不同的零点,且这些零点之和为-2,求a、b的值;
(3)若函数![]() 在
在![]() 上有四个不同零点
上有四个不同零点![]() ,求
,求![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
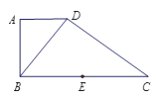
【题目】如图,在直角梯形![]() 中,
中, ![]() //
// ![]() ,
, ![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() , 点
, 点![]() 是
是![]() 边的中点, 将△
边的中点, 将△![]() 沿
沿![]() 折起,使平面
折起,使平面![]() ⊥平面
⊥平面![]() ,连接
,连接![]() ,
, ![]() ,
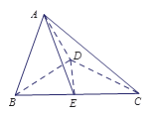
, ![]() , 得到如
, 得到如
图所示的空间几何体.
(Ⅰ)求证: ![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,学校决定利用随机数表法从中抽取100人进行成绩抽样调查,先将800人按001,002,…,800进行编号.
(1)如果从第8行第7列的数开始向右读,请你依次写出最先检查的3个人的编号;
(下面摘取了第7行到第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
(2)抽取的100人的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42.
人数 | 数学 | |||
优秀 | 良好 | 及格 | ||
| 优秀 | 7 | 20 | 5 |
良好 | 9 | 18 | 6 | |
及格 | a | 4 | b | |
①若在该样本中,数学成绩优秀率是30%,求a,b的值:
②在地理成绩及格的学生中,已知![]() 求数学成绩优秀的人数比及格的人数少的概率.
求数学成绩优秀的人数比及格的人数少的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]()
(l)设![]() 为参数,若
为参数,若![]() ,求直线
,求直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 设
设![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,某小区中有条长为50米,宽为6.5米的道路ABCD,在路的一侧可以停放汽车,已知小型汽车的停车位是一个2.5米宽,5米长的矩形,如GHPQ,这样该段道路可以划岀10个车位,随着小区居民汽车拥有量的增加,停车难成为普遍现象.经过各方协商,小区物业拟压缩绿化,拓宽道路,改变车位方向增加停车位,如图2,改建后的通行宽度保持不变,即G到AD的距离不变.
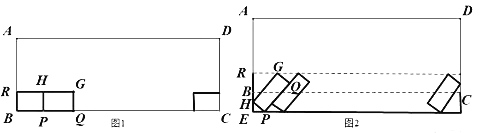
(1)绿化被压缩的宽度BE与停车位的角度∠HPE有关,记![]() 为停车方便,要求
为停车方便,要求![]() ,写出
,写出![]() 关于
关于![]() 的函数表达式
的函数表达式![]() ;
;
(2)沿用(1)的条件和记号,实际施工时,BE=3米,问改造后的停车位增加了多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com