
【题目】已知![]() ,其中
,其中![]() .
.
(1)若![]() ,写出
,写出![]() 的单调区间:
的单调区间:
(2)若函数![]() 恰有三个不同的零点,且这些零点之和为-2,求a、b的值;
恰有三个不同的零点,且这些零点之和为-2,求a、b的值;
(3)若函数![]() 在
在![]() 上有四个不同零点
上有四个不同零点![]() ,求
,求![]() 的最大值。
的最大值。
【答案】(1)![]() 递减,
递减,![]() 递增;(2)
递增;(2)![]() ;(3)4
;(3)4
【解析】
(1)由![]() ,得出函数的解析式
,得出函数的解析式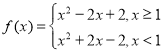 ,再做出图像可得函数
,再做出图像可得函数![]() 的单调区间;
的单调区间;
(2)令![]() ,即
,即![]() 或
或![]() ,再由
,再由![]() ,可得方程
,可得方程![]() 中有两个不等的实根,要使函数
中有两个不等的实根,要使函数![]() 恰有三个不同的零点,且这些零点之和为-2,,则需方程
恰有三个不同的零点,且这些零点之和为-2,,则需方程![]() 有两个相等的实根,可建立关于的方程,解之可得
有两个相等的实根,可建立关于的方程,解之可得![]() 的值;
的值;
(3)由![]() ,即
,即![]() 或
或![]() ,设
,设![]() 的两根为
的两根为![]() ,并且可得
,并且可得![]() ,
,![]() 的两根为
的两根为![]() ,并且可得
,并且可得![]() ,所以
,所以![]() 两根中一正一负,再由
两根中一正一负,再由![]() 均在
均在![]() 内,得
内,得![]() 的负根
的负根![]() ,从而可得
,从而可得![]() 的最大值.
的最大值.
(1)当![]() 时,
时,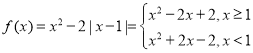 ,做出图像如下图1所示,
,做出图像如下图1所示,
所以![]() 的单调区间是:在
的单调区间是:在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
(2)令![]() ,即
,即![]() ,所以
,所以![]() 或
或![]() ,
,
整理得![]() 或
或![]() ,
,
因为![]() ,所以方程
,所以方程![]() 中
中![]() 恒成立,也即是
恒成立,也即是![]() 一定有两个不等的实根,
一定有两个不等的实根,
设这两个实根为![]() 并且
并且![]() ,要使函数
,要使函数![]() 恰有三个不同的零点,且这些零点之和为-2,
恰有三个不同的零点,且这些零点之和为-2,
现需方程![]() 有两个相等的实根,设此根为
有两个相等的实根,设此根为![]() ,且
,且![]() ,
,
所以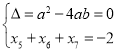 ,即
,即 ,解得
,解得![]() ,
,
所以![]() 的值为
的值为![]() ;
;
(3)若![]() ,即
,即![]() 或
或![]() ,
,
设![]() 的两根为
的两根为![]() ,则
,则![]() ,
,
![]() 的两根为
的两根为![]() ,则
,则![]() ,所以
,所以![]() 两根中一正一负,
两根中一正一负,
![]() ,
,
![]() 均在
均在![]() 内,
内,![]() 的负根
的负根![]() 在
在![]() 内,
内,
![]() ,
,![]() ,
,
所以![]() 的最大值为4.
的最大值为4.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
【题目】定义:若函数![]() 的图像经过变换
的图像经过变换![]() 后所得的图像对应的函数与
后所得的图像对应的函数与![]() 的值域相同,则称变换
的值域相同,则称变换![]() 是
是![]() 的同值变换,下面给出了四个函数与对应的变换:
的同值变换,下面给出了四个函数与对应的变换:
①![]() 将函数
将函数![]() 的图像关于
的图像关于![]() 轴作对称变换;
轴作对称变换;
②![]() 将函数
将函数![]() 的图像关于
的图像关于![]() 轴作对称变换;
轴作对称变换;
③![]() 将函数
将函数![]() 的图像关于点(-1,1)作对称变换;
的图像关于点(-1,1)作对称变换;
④![]() 将函数
将函数![]() 的图像关于点(-1,0)作对称变换;
的图像关于点(-1,0)作对称变换;
其中![]() 是
是![]() 的同值变换的有_______.(写出所有符合题意的序号)
的同值变换的有_______.(写出所有符合题意的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义运算“![]() ”:对于任意
”:对于任意![]() ,
,![]() (等式的右边是通常的加减乘运算).若数列
(等式的右边是通常的加减乘运算).若数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() 对任意
对任意![]() 都成立.
都成立.
(1)求![]() 的值,并推导出用
的值,并推导出用![]() 表示
表示![]() 的解析式;
的解析式;
(2)若![]() ,令
,令![]() ,证明数列
,证明数列![]() 是等差数列;
是等差数列;
(3)若![]() ,令
,令![]() ,数列
,数列![]() 满足
满足![]() ,求正实数b的取值范围.
,求正实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术·均输》中有如下问题:“今有五人分十钱,令上二人所得与下三人等,问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分10钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列,问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,甲所得为( )
A.![]() 钱B.
钱B.![]() 钱C.
钱C.![]() 钱D.
钱D.![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是定义在区间
是定义在区间![]() 上且同时满足如下条件的函数
上且同时满足如下条件的函数![]() 所组成的集合:
所组成的集合:
①对任意的![]() ,都有
,都有![]() ;
;
②存在常数![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]()
(1)设![]() ,试判断
,试判断![]() 是否属于集合
是否属于集合![]() ;
;
(2)若![]() ,如果存在
,如果存在![]() ,使得
,使得![]() ,求证:满足条件的
,求证:满足条件的![]() 是唯一的;
是唯一的;
(3)设![]() ,且
,且![]() ,试求参数
,试求参数![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,集合
,集合![]() ,集合
,集合![]() .
.
(1)用列举法表示集合C;
(2)设集合C的含n个元素所有子集为![]() ,记有限集合M的所有元素和为
,记有限集合M的所有元素和为![]() ,求
,求![]()
![]() 的值;
的值;
(3)已知集合P、Q是集合C的两个不同子集,若P不是Q的子集,且Q不是P的子集,求所有不同的有序集合对![]() 的个数
的个数![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过多年的运作,“双十一”抢购活动已经演变成为整个电商行业的大型集体促销盛宴.为迎接2014年“双十一”网购狂欢节,某厂家拟投入适当的广告费,对网上所售产品进行促销.经调查测算,该促销产品在“双十一”的销售量p万件与促销费用x万元满足![]() (其中
(其中![]() ,a为正常数).已知生产该产品还需投入成本
,a为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为
![]() 元/件,假定厂家的生产能力完全能满足市场的销售需求.
元/件,假定厂家的生产能力完全能满足市场的销售需求.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中真命题的序号为(少填或错填均不得分)______.若一个球的半径缩小为原来的一半,则其体积缩小为原来的八分之一;②若两组数据的平均值相等,则它们的标准差也相等;③直线![]() 与圆
与圆![]() 相切;④若两个平面都垂直于同一个平面,则这两个平面平行.
相切;④若两个平面都垂直于同一个平面,则这两个平面平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设计一个随机试验,使一个事件的概率与某个未知数有关,然后通过重复试验,以频率估计概率,即可求得未知数的近似解,这种随机试验在数学上称为随机模拟法,也称为蒙特卡洛法。比如要计算一个正方形内部不规则图形的面积,就可以利用撒豆子,计算出落在不规则图形内部和正方形内部的豆子数比近似等于不规则图形面积与正方形面积比,从而近似求出不规则图形的面积.
统计学上还有一个非常著名的蒲丰投针实验:平面上间隔![]() 的平行线,向平行线间的平面上任意投掷一枚长为
的平行线,向平行线间的平面上任意投掷一枚长为![]() 的针
的针![]() ,通过多次实验可以近似求出针与任一平行线(以
,通过多次实验可以近似求出针与任一平行线(以![]() 为例)相交(当针的中点在平行线外不算相交)的概率.以
为例)相交(当针的中点在平行线外不算相交)的概率.以![]() 表示针的中点与最近一条平行线
表示针的中点与最近一条平行线![]() 的距离,又以
的距离,又以![]() 表示
表示![]() 与
与![]() 所成夹角,如图甲,易知满足条件:
所成夹角,如图甲,易知满足条件:![]() ,
,![]() .
.
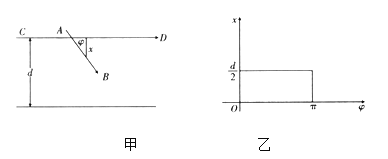
由这两式可以确定平面上的一个矩形![]() ,如图乙,在图甲中,当
,如图乙,在图甲中,当![]() 满足___________(
满足___________(![]() 与
与![]() ,
,![]() 之间的关系)时,针与平行线相交(记为事件
之间的关系)时,针与平行线相交(记为事件![]() ).可用从实验中获得的频率去近似
).可用从实验中获得的频率去近似![]() ,即投针
,即投针![]() 次,其中相交的次数为
次,其中相交的次数为![]() ,则
,则![]() ,历史上有一个数学家亲自做了这实验,他投掷的次数是5000,相交的次数为2550次,
,历史上有一个数学家亲自做了这实验,他投掷的次数是5000,相交的次数为2550次,![]() ,
,![]() ,依据这个实验求圆周率
,依据这个实验求圆周率![]() 的近似值_________.(精确到3位小数)
的近似值_________.(精确到3位小数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com