
【题目】![]() 是定义在区间
是定义在区间![]() 上且同时满足如下条件的函数
上且同时满足如下条件的函数![]() 所组成的集合:
所组成的集合:
①对任意的![]() ,都有
,都有![]() ;
;
②存在常数![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]()
(1)设![]() ,试判断
,试判断![]() 是否属于集合
是否属于集合![]() ;
;
(2)若![]() ,如果存在
,如果存在![]() ,使得
,使得![]() ,求证:满足条件的
,求证:满足条件的![]() 是唯一的;
是唯一的;
(3)设![]() ,且
,且![]() ,试求参数
,试求参数![]() 的取值范围
的取值范围
【答案】(1)是![]() 的元素;(2)证明见解析;(3)
的元素;(2)证明见解析;(3)![]()
【解析】
(1)构造函数f(x)=φ(x)![]() x
x![]() x2
x2![]() x+1,判断单调性求最值即可证明
x+1,判断单调性求最值即可证明
(2)要证明唯一性通过反证法来证明,假设满足这样条件的x0有两个,导出矛盾.
(3)转化为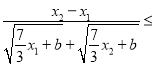 c(x2﹣x1)恒成立,利用单调性求最值求解
c(x2﹣x1)恒成立,利用单调性求最值求解
(1)x∈[1,2],所以φ(x)∈(![]() ,
,![]() )
)
令f(x)=φ(x)![]() x
x![]() x2
x2![]() x+1,则f'(x)
x+1,则f'(x)![]() x
x![]() ,
,
因为x∈[1,2],所以f'(x)≤0,所以f(x)在[1,2]上单调递减,
对任意1≤x1≤x2≤2,f(x1)≤f(x2)φ(x2)﹣φ(x1)![]() (x2﹣x1)|φ(x1)﹣φ(x2)|
(x2﹣x1)|φ(x1)﹣φ(x2)|![]() |x1﹣x2|,即存在
|x1﹣x2|,即存在![]()
所以φ(x)∈A.
(2)假设存在不同的两个数a、b∈(1,2),使得φ(a)=a,φ(b)=b,
因为φ(x)∈A,所以|φ(a)﹣φ(b)|=|a﹣b|≤c|a﹣b|,
因为a≠b,所以|a﹣b|>
所以满足x0=φ(x0)的x0是唯一的.
(3)因为φ(x)单调递增,故φ(x)∈(1,2),所以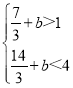 ,解得b∈(
,解得b∈(![]() ,
,![]() );
);
对任意1≤x1≤x2≤2,|φ(x1)﹣φ(x2)|![]()
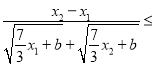 c(x2﹣x1)
c(x2﹣x1)
所以![]() 对任意1≤x1≤x2≤2恒成立,
对任意1≤x1≤x2≤2恒成立,
所以![]() b
b![]() .
.
综上b∈(![]() ,
,![]() ).
).


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
【题目】若存在常数![]()
![]() ,使得数列
,使得数列![]() 满足
满足![]() 对一切
对一切![]() 恒成立,则称
恒成立,则称![]() 为可控数列,
为可控数列,![]() .
.
(1)若![]() ,
,![]() ,问
,问![]() 有多少种可能?
有多少种可能?
(2)若![]() 是递增数列,
是递增数列,![]() ,且对任意的
,且对任意的![]() ,数列
,数列![]() ,
,![]() ,
,![]()
![]() 成等差数列,判断
成等差数列,判断![]() 是否为可控数列?说明理由;
是否为可控数列?说明理由;
(3)设单调的可控数列![]() 的首项
的首项![]() ,前
,前![]() 项和为
项和为![]() ,即
,即![]() .问
.问![]() 的极限是否存在,若存在,求出
的极限是否存在,若存在,求出![]() 与
与![]() 的关系式;若不存在,请说明理由.
的关系式;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)设椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 、
、![]() ,
,![]() 是椭圆
是椭圆![]() 与双曲线
与双曲线![]() 的公共点,且△
的公共点,且△![]() 的周长为6,求椭圆
的周长为6,求椭圆![]() 的方程;我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”;
的方程;我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”;
(2)如图,已知“盾圆![]() ”的方程为
”的方程为![]() ,设“盾圆
,设“盾圆![]() ”上的任意一点
”上的任意一点![]() 到
到![]() 的距离为
的距离为![]() ,
,![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求证:
,求证:![]() 为定值;
为定值;
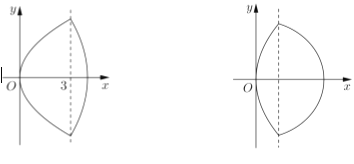
(3)由抛物线弧![]() (
(![]() )与第(1)小题椭圆弧
)与第(1)小题椭圆弧![]()
![]() (
(![]() )所合成的封闭曲线为“盾圆
)所合成的封闭曲线为“盾圆![]() ”,设过点
”,设过点![]() 的直线与“盾圆
的直线与“盾圆![]() ”交于
”交于![]() 、
、![]() 两点,
两点,![]() ,
,![]() ,且
,且![]() (
(![]() ),试用
),试用![]() 表示
表示![]() ,并求
,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,其中
,其中![]() .
.
(1)若![]() ,写出
,写出![]() 的单调区间:
的单调区间:
(2)若函数![]() 恰有三个不同的零点,且这些零点之和为-2,求a、b的值;
恰有三个不同的零点,且这些零点之和为-2,求a、b的值;
(3)若函数![]() 在
在![]() 上有四个不同零点
上有四个不同零点![]() ,求
,求![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
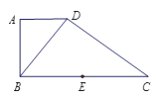
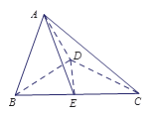
【题目】如图,在直角梯形![]() 中,
中, ![]() //
// ![]() ,
, ![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() , 点
, 点![]() 是
是![]() 边的中点, 将△
边的中点, 将△![]() 沿
沿![]() 折起,使平面
折起,使平面![]() ⊥平面
⊥平面![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() , 得到如
, 得到如
图所示的空间几何体.
(Ⅰ)求证: ![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,学校决定利用随机数表法从中抽取100人进行成绩抽样调查,先将800人按001,002,…,800进行编号.
(1)如果从第8行第7列的数开始向右读,请你依次写出最先检查的3个人的编号;
(下面摘取了第7行到第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
(2)抽取的100人的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42.
人数 | 数学 | |||
优秀 | 良好 | 及格 | ||
| 优秀 | 7 | 20 | 5 |
良好 | 9 | 18 | 6 | |
及格 | a | 4 | b | |
①若在该样本中,数学成绩优秀率是30%,求a,b的值:
②在地理成绩及格的学生中,已知![]() 求数学成绩优秀的人数比及格的人数少的概率.
求数学成绩优秀的人数比及格的人数少的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义![]() ,已知函数
,已知函数![]() 、
、![]() 定义域都是
定义域都是![]() ,给出下列命题:
,给出下列命题:
(1)若![]() 、
、![]() 都是奇函数,则函数
都是奇函数,则函数![]() 为奇函数;
为奇函数;
(2)若![]() 、
、![]() 都是减函数,则函数
都是减函数,则函数![]() 为减函数;
为减函数;
(3)若![]() ,
,![]() ,则
,则![]() ;
;
(4)若![]() 、
、![]() 都是周期函数,则函数
都是周期函数,则函数![]() 是周期函数.
是周期函数.
其中正确命题的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com