
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)设函数![]() 若至少存在一个
若至少存在一个![]() ,使得
,使得![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)求导后代入![]() 求得
求得![]() 在
在![]() 处的切线斜率,再利用点斜式求得切线方程即可.
处的切线斜率,再利用点斜式求得切线方程即可.
(2)求导后分![]() 与
与![]() 时,分析单调性再根据函数性质的最值满足的条件列式求不等式即可.
时,分析单调性再根据函数性质的最值满足的条件列式求不等式即可.
(1)当![]() 时,
时,![]() ,
,
∴![]() ,即切线斜率为2,故由点斜式方程可得切线方程为
,即切线斜率为2,故由点斜式方程可得切线方程为![]() ,即
,即![]()
(2)原问题等价于至少存在一个![]() ,使得
,使得![]() 成立,
成立,
令![]() ,
,![]() 则
则![]() ,
,
①当![]() 时,
时,![]() ,则函数h(x)在[1,e]上单调递减,故h(x)min=h(e)=﹣2<0,符合题意;
,则函数h(x)在[1,e]上单调递减,故h(x)min=h(e)=﹣2<0,符合题意;
②当![]() 时,令,
时,令,![]() ,解得
,解得![]() ,则函数h(x)在
,则函数h(x)在![]() 上单调递减,令
上单调递减,令![]() ,解得
,解得![]() ,则函数h(x)在
,则函数h(x)在![]() 单调递增,
单调递增,
且![]() ,
,![]() ,
,![]()
1.当![]() ,即
,即![]() 时,在
时,在![]() 上
上![]() ,
,![]() 单调递增,
单调递增,
此时![]() 不符合题意
不符合题意
2.当![]() ,即
,即![]() 时, 在
时, 在![]() 上
上![]() ,
,![]() 单调递减,
单调递减,
此时![]() 满足题意
满足题意
3.当![]() ,即
,即![]() 时,
时,![]() ,不满足题意
,不满足题意
综上,实数a的取值范围为![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西![]() 且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以
且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以![]() 海里/小时的航行速度匀速行驶,经过
海里/小时的航行速度匀速行驶,经过![]() 小时与轮船相遇。
小时与轮船相遇。
(1)若![]() 小时,小艇与轮船恰好相遇,求小艇速度的大小和方向;(角度精确到
小时,小艇与轮船恰好相遇,求小艇速度的大小和方向;(角度精确到![]() );
);
(2)为保证小艇在90分钟内(含90分钟)能与轮船相遇,试确定小艇航行速度的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
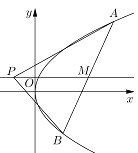
【题目】如图,已知点![]() 是
是![]() 轴左侧(不含
轴左侧(不含![]() 轴)一点,抛物线
轴)一点,抛物线![]() 上存在不同的两点
上存在不同的两点![]() 、
、![]() ,满足
,满足![]() 、
、![]() 的中点均在抛物线
的中点均在抛物线![]() 上.
上.
(1)求抛物线![]() 的焦点到准线的距离;
的焦点到准线的距离;
(2)设![]() 中点为
中点为![]() ,且
,且![]() ,
,![]() ,证明:
,证明:![]() ;
;
(3)若![]() 是曲线
是曲线![]() (
(![]() )上的动点,求
)上的动点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的方程为
的方程为![]() ,过原点作斜率为
,过原点作斜率为![]() 的直线和曲线
的直线和曲线![]() 相交,另一个交点记为
相交,另一个交点记为![]() ,过
,过![]() 作斜率为
作斜率为![]() 的直线和曲线
的直线和曲线![]() 相交,另一个交点记为
相交,另一个交点记为![]() ,过
,过![]() 作斜率为
作斜率为![]() 的直线和曲线
的直线和曲线![]() 相交,另一个交点记为
相交,另一个交点记为![]() ,……,如此下去,一般地,过
,……,如此下去,一般地,过![]() 作斜率为
作斜率为![]() 的直线和曲线
的直线和曲线![]() 相交,另一个交点记为
相交,另一个交点记为![]() ,设点
,设点![]() .
.
(1)指出![]() ,并求
,并求![]() 与
与![]() 的关系式
的关系式![]() ;
;
(2)求![]() 的通项公式,并指出点列
的通项公式,并指出点列![]() ,
,![]() ,……,
,……,![]() ,……向哪一点无限接近?说明理由;
,……向哪一点无限接近?说明理由;
(3)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,设
,设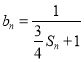 ,求所有可能的乘积
,求所有可能的乘积![]() 的和.
的和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义运算“![]() ”:对于任意
”:对于任意![]() ,
,![]() (等式的右边是通常的加减乘运算).若数列
(等式的右边是通常的加减乘运算).若数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() 对任意
对任意![]() 都成立.
都成立.
(1)求![]() 的值,并推导出用
的值,并推导出用![]() 表示
表示![]() 的解析式;
的解析式;
(2)若![]() ,令
,令![]() ,证明数列
,证明数列![]() 是等差数列;
是等差数列;
(3)若![]() ,令
,令![]() ,数列
,数列![]() 满足
满足![]() ,求正实数b的取值范围.
,求正实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是定义在区间
是定义在区间![]() 上且同时满足如下条件的函数
上且同时满足如下条件的函数![]() 所组成的集合:
所组成的集合:
①对任意的![]() ,都有
,都有![]() ;
;
②存在常数![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]()
(1)设![]() ,试判断
,试判断![]() 是否属于集合
是否属于集合![]() ;
;
(2)若![]() ,如果存在
,如果存在![]() ,使得
,使得![]() ,求证:满足条件的
,求证:满足条件的![]() 是唯一的;
是唯一的;
(3)设![]() ,且
,且![]() ,试求参数
,试求参数![]() 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com