
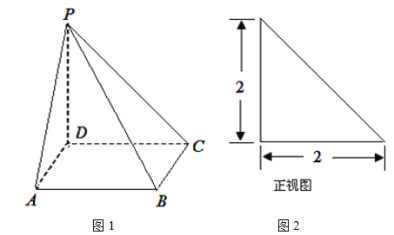
【题目】如图1,四棱锥![]() 的底面
的底面![]() 是正方形,
是正方形,![]() 垂直于底面
垂直于底面![]() ,已知四棱锥的正视图,如图2所示.
,已知四棱锥的正视图,如图2所示.
(I)若M是![]() 的中点,证明:
的中点,证明:![]() 平面
平面![]() ;
;
(II)求棱锥![]() 的体积.
的体积.
【答案】(I)证明见解析;(II)![]() .
.
【解析】
(Ⅰ)由正视图可知,![]() 先证明
先证明![]() 平面
平面![]() 得到
得到![]() .由等腰三角形可得
.由等腰三角形可得![]() ,利用线面垂直的判定定理可得结果; (Ⅱ)在平面PCD内过M作
,利用线面垂直的判定定理可得结果; (Ⅱ)在平面PCD内过M作![]() 交CD于N,可得棱锥
交CD于N,可得棱锥![]() 的体积,结合棱锥
的体积,结合棱锥![]() 的体积等于棱锥
的体积等于棱锥![]() 的体积,从而可得结果.
的体积,从而可得结果.
(Ⅰ)由正视图可知,![]()
∵PD⊥平面ABCD,∴ PD⊥BC
又∵ABCD是正方形,∴BC⊥CD.
∵![]() ,∴BC⊥平面PCD
,∴BC⊥平面PCD
∵![]() 平面PCD,∴DM⊥BC.
平面PCD,∴DM⊥BC.
又![]() 是等腰三角形,E是斜边PC的中点,所以∴DM⊥PC
是等腰三角形,E是斜边PC的中点,所以∴DM⊥PC
又∵![]() ,∴DM⊥平面PBC.
,∴DM⊥平面PBC.
(Ⅱ)在平面PCD内过M作MN//PD交CD于N,所以![]() 且
且![]() 平面ABCD,所以棱锥M-ABD的体积为
平面ABCD,所以棱锥M-ABD的体积为
![]()
又∵棱锥A-BDM的体积等于棱锥M-ABD的体积,
∴棱锥A-BDM的体积等于![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】《九章算术·均输》中有如下问题:“今有五人分十钱,令上二人所得与下三人等,问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分10钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列,问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,甲所得为( )
A.![]() 钱B.
钱B.![]() 钱C.
钱C.![]() 钱D.
钱D.![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,集合
,集合![]() ,集合
,集合![]() .
.
(1)用列举法表示集合C;
(2)设集合C的含n个元素所有子集为![]() ,记有限集合M的所有元素和为
,记有限集合M的所有元素和为![]() ,求
,求![]()
![]() 的值;
的值;
(3)已知集合P、Q是集合C的两个不同子集,若P不是Q的子集,且Q不是P的子集,求所有不同的有序集合对![]() 的个数
的个数![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过多年的运作,“双十一”抢购活动已经演变成为整个电商行业的大型集体促销盛宴.为迎接2014年“双十一”网购狂欢节,某厂家拟投入适当的广告费,对网上所售产品进行促销.经调查测算,该促销产品在“双十一”的销售量p万件与促销费用x万元满足![]() (其中
(其中![]() ,a为正常数).已知生产该产品还需投入成本
,a为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为
![]() 元/件,假定厂家的生产能力完全能满足市场的销售需求.
元/件,假定厂家的生产能力完全能满足市场的销售需求.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
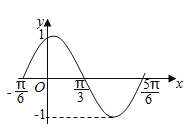
【题目】如图是函数![]() 在区间
在区间![]() 上的图象,为了得到这个函数的图象,只需将
上的图象,为了得到这个函数的图象,只需将![]() 的图象上的所有的点( )
的图象上的所有的点( )
![]()
A.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
B.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
C.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
D.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中真命题的序号为(少填或错填均不得分)______.若一个球的半径缩小为原来的一半,则其体积缩小为原来的八分之一;②若两组数据的平均值相等,则它们的标准差也相等;③直线![]() 与圆
与圆![]() 相切;④若两个平面都垂直于同一个平面,则这两个平面平行.
相切;④若两个平面都垂直于同一个平面,则这两个平面平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 满足:对一切
满足:对一切![]() ,有
,有![]() ,其中
,其中![]() 是与
是与![]() 无关的常数,称数列上有界(有上界),并称
无关的常数,称数列上有界(有上界),并称![]() 是它的一个上界,对一切
是它的一个上界,对一切![]() ,有
,有![]() ,其中
,其中![]() 是与
是与![]() 无关的常数,称数列下有界(有下界),并称
无关的常数,称数列下有界(有下界),并称![]() 是它的一个下界.一个数列既有上界又有下界,则称为有界数列,常值数列是一个特殊的有界数列.设
是它的一个下界.一个数列既有上界又有下界,则称为有界数列,常值数列是一个特殊的有界数列.设![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)若数列![]() 为常数列,试求实数
为常数列,试求实数![]() 、
、![]() 满足的等式关系,并求出实数
满足的等式关系,并求出实数![]() 的取值范围;
的取值范围;
(2)下面四个选项,对一切实数![]() ,恒正确的是.(写出所有正确选项,不需要证明其正确,但需要简单说明一下为什么不选余下几个)
,恒正确的是.(写出所有正确选项,不需要证明其正确,但需要简单说明一下为什么不选余下几个)
A. 当![]() 时,
时,![]() B. 当
B. 当![]() 时,
时,![]()
C. 当![]() 时,
时,![]() D. 当
D. 当![]() 时,
时,![]()
(3)若![]() ,
,![]() ,且数列
,且数列![]() 是有界数列,求
是有界数列,求![]() 的值及
的值及![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com