
过抛物线![]() =x的顶点O作两条互相垂直的弦OA、OB.
=x的顶点O作两条互相垂直的弦OA、OB.
(1)求证:直线AB过定点M(1,0);
(2)求△ABO面积的最小值.
(1)证明 设A( 则 ①若 ②若 由OA⊥OB,得 又 ∴ 故AB方程为y- 即( 化简得( (2)解:直线AB:x-1=ty与 ∴ ∴ ∴ ∴ 当t=0即AB⊥x轴时, 点评 (1)除了选用点参数外,还可设OA方程为y=kx,即选用OA斜率为参数;(2)中在设AB的方程时,若设成y=k(x-1),则需讨论.
|


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2007年上海市高三教学质量检测数学试卷(理) 题型:044
已知动点M到定点(1,0)的距离比M到定直线x=-2的距离小1.
(1)求证:M点轨迹为抛物线,并求出其轨迹方程;
(2)大家知道,过圆上任意一点P,任意作相互垂直的弦PA,PB,则弦AB必过圆心(定点),受此启发,研究下面的问题:
①过(1)中的抛物线的顶点O任作相互垂直的弦OA,OB,则弦AB是否经过一个定点?若经过定点(设为Q),请求出Q点的坐标,否则说明理由;
②研究:对于抛物线y2=2px上顶点以外的定点是否也有这样的性质?请提出一个一般的结论,并证明.
查看答案和解析>>
科目:高中数学 来源:2014届江西省高二第二次月考文科数学试卷(解析版) 题型:解答题
(本小题13分)曲线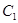 上任意一点M满足
上任意一点M满足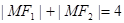 ,
其中F
,
其中F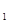 (-
(-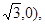 F
F (
(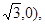 抛物线
抛物线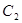 的焦点是直线y=x-1与x轴的交点, 顶点为原点O.
的焦点是直线y=x-1与x轴的交点, 顶点为原点O.
(1)求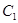 ,
,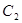 的标准方程;
的标准方程;
(2)请问是否存在直线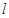 满足条件:①过
满足条件:①过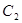 的焦点
的焦点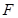 ;②与
;②与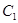 交于不同
交于不同
两点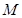 ,
,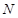 ,且满足
,且满足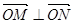 ?若存在,求出直线
?若存在,求出直线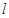 的方程;若不
的方程;若不
存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
边长为1的等边三角形AOB,O为坐标原点,AB⊥x轴,以O为顶点且过A、B的抛物线方程是( )
(A)y2=![]() x (B)y2=-
x (B)y2=-![]() x
x
(C)y2=±![]() x (D) y2=±
x (D) y2=±![]() x
x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com