
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(Ⅱ)(i)求出函数的导数,通过讨论a的范围,根据函数的零点的个数,求出a的范围即可;
(ii)根据a的范围,得到$\frac{{{x}_{1}e}^{{x}_{1}}}{{{(x}_{1}+1)}^{2}}$=$\frac{{{x}_{2}e}^{{x}_{2}}}{{{(x}_{2}+1)}^{2}}$=-$\frac{1}{a}$,令m>0,得到F (=1+m)-F(-1-m)=$\frac{m+1}{{{m}^{2}e}^{m+1}}$($\frac{m-1}{m+1}$e2m+1),再令φ(m)=$\frac{m-1}{m+1}$e2m+1,根据函数的单调性证明即可.
解答 解:(Ⅰ)F(x)=$\frac{f(x)}{g(x)}$=$\frac{{xe}^{x}}{{(x+1)}^{2}}$,(x≠-1),
F′(x)=$\frac{(x+1{)e}^{x}{•(x+1)}^{2}-{xe}^{x}•2(x+1)}{{(x+1)}^{4}}$=$\frac{{e}^{x}{(x}^{2}+1)}{{(x+1)}^{3}}$,
∴x∈(-∞,-1)时,F′(x)<0,F(x)递减,
x∈(-1,+∞)时,F′(x)>0,F(x)递增;
(Ⅱ)由已知,G(x)=af(x)+g(x)=axex+(x+1)2,
G′(x)=a(x+1)ex+2(x+1)=(x+1)(aex+2),
(i)①a=0时,G(x)=(x+1)2,有唯一零点-1,
②a>0时,aex+2>0,
∴x∈(-∞,-1)时,G′(x)<0,G(x)递减,
x∈(-1,+∞)时,G′(x)>0,G(x)递增,
∴G(x)极小值=G(-1)=-$\frac{a}{e}$<0,
∵G(0)=1>0,∴x∈(-1,+∞)时,G(x)有唯一零点,
x<-1时,ax<0,则ex<$\frac{1}{e}$,∴axex>$\frac{ax}{e}$,
∴G(x)>$\frac{ax}{e}$+(x+1)2=x2+(2+$\frac{a}{e}$)x+1,
∵△=${(2+\frac{a}{e})}^{2}$-4×1×1=$\frac{4a}{e}$+${(\frac{a}{e})}^{2}$>0,
∴?t1,t2,且t1<t2,当x∈(-∞,t1),(t2,+∞)时,
使得x2+(2+$\frac{a}{e}$)x+1>0,
取x0∈(-∞,-1),则G(x0)>0,则x∈(-∞,-1)时,G(x)有唯一零点,
即a>0时,函数G(x)有2个零点;
③a<0时,G′(x)=a(x+1)(ex-(-$\frac{2}{a}$)),
由G′(x)=0,得x=-1或x=ln(-$\frac{2}{a}$),
若-1=ln(-$\frac{2}{a}$),即a=-2e时,G′(x)≤0,G(x)递减,至多1个零点;
若-1>ln(-$\frac{2}{a}$),即a<-2e时,G′(x)=a(x+1)(ex-(-$\frac{2}{a}$)),
注意到y=x+1,y=ex+$\frac{2}{a}$都是增函数,
∴x∈(-∞,ln(-$\frac{2}{a}$))时,G′(x)<0,G(x)是减函数,
x∈(ln(-$\frac{2}{a}$),-1)时,G′(x)>0,G(x)递增,
x∈(-1,+∞)时,G′(x)<0,G(x)递减,
∵G(x)极小值=G(ln(-$\frac{2}{a}$))=ln2(-$\frac{2}{a}$)+1>0,
∴G(x)至多1个零点;
若-1<ln(-$\frac{2}{a}$),即a>-2e时,
x∈(-∞,-1)时,G′(x)<0,G(x)是减函数,
x∈(-1,ln(-$\frac{2}{a}$))时,G′(x)>0,G(x)递增,
x∈(ln(-$\frac{2}{a}$),+∞)时,G′(x)<0,G(x)递减,
∵G(x)极小值=G(-1)=-$\frac{a}{e}$>0,
∴G(x)至多1个零点;
综上,若函数G(x)有2个零点,
则参数a的范围是(0,+∞);
(ii)由(i)得:函数G(x)有2个零点,则参数a的范围是(0,+∞),
x1,x2是G(x)的两个零点,则有:
$\left\{\begin{array}{l}{G{(x}_{1})=0}\\{G{(x}_{2})=0}\end{array}\right.$,即$\left\{\begin{array}{l}{{{ax}_{1}e}^{{x}_{1}}{+{(x}_{1}+1)}^{2}=0}\\{{{ax}_{2}e}^{{x}_{2}}{+{(x}_{2}+1)}^{2}=0}\end{array}\right.$,即$\frac{{{x}_{1}e}^{{x}_{1}}}{{{(x}_{1}+1)}^{2}}$=$\frac{{{x}_{2}e}^{{x}_{2}}}{{{(x}_{2}+1)}^{2}}$=-$\frac{1}{a}$,
∵F(x)=$\frac{{xe}^{x}}{{(x+1)}^{2}}$,则F(x1)=F(x2)<0,且x1<0,x1≠-1,x2<0,x2≠-1,x1≠x2,
由(Ⅰ)知,当x∈(-∞,-1)时,F(x)是减函数,x∈(-1,+∞)时,F(x)是增函数,
令m>0,F (=1+m)-F(-1-m)=$\frac{m+1}{{{m}^{2}e}^{m+1}}$($\frac{m-1}{m+1}$e2m+1),
再令φ(m)=$\frac{m-1}{m+1}$e2m+1=e2m-$\frac{{2e}^{2m}}{m+1}$-1,
则φ′(m)=$\frac{{{2m}^{2}e}^{2m}}{{(m+1)}^{2}}$>0,
∴φ(m)>φ(0)=0,又$\frac{m+1}{{{m}^{2}e}^{2m}}$>0,
m>0时,F(-1+m)-F(-1-m)>0恒成立,
即F(-1+m)>F(-1-m)恒成立,
令m=-1-x1>0,即x1<-1,有F(-1+(-1-x1))>F(-1-(-1-x1)),
即F(-2-x1)>F(x1)=F(x2),
∵x1<-1,∴-2-x1>-1,又F(x1)=F(x2),必有x2>-1,
当x∈(-1,+∞)时,F(x)是增函数,
∴-2-x1>x2,
即x1+x2+2<0.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,考查转化思想,是一道综合题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
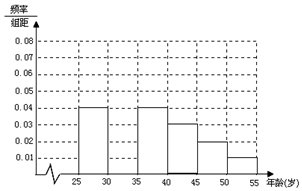 智能手机功能强大,许多人喜欢用手机看电视、看电影.某同学在暑假期间开展社会实践,对[25,55]岁的人群随机抽取1000人调查是否喜欢用手机看电视、看电影,对喜欢用手机看电视、看电影的称为“手机族”,得到如下各年龄段“手机族”人数频率分布直方图:
智能手机功能强大,许多人喜欢用手机看电视、看电影.某同学在暑假期间开展社会实践,对[25,55]岁的人群随机抽取1000人调查是否喜欢用手机看电视、看电影,对喜欢用手机看电视、看电影的称为“手机族”,得到如下各年龄段“手机族”人数频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{π^2}$ | B. | $1-\frac{4}{π^2}$ | C. | $\frac{4}{π^2}$ | D. | $1-\frac{2}{π^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $1-\frac{π}{6}$ | D. | $1-\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com