【题目】大学毕业生小王相应国家“自主创业”的号召，利用银行小额无息贷款开办了一家饰品店，该店购进一种今年新上市的饰品进行销售，饰品的进价为每件40元，售价为每件60元，每月可卖出300件，市场调查反映：调整价格时，售价每涨1元每月要少卖10件；售价每下降1元每月多卖20件，为获得更大的利润，现将饰品售价调整为（元/件）（即售价上涨，即售价下降），每月饰品销售为（件），月利润为（元）.

（1）直接写出与之间的函数关系式；

（2）如何确定销售价格才能使月利润最大？求最大月利润；

（3）为了使每月利润不少于6000元，应如何控制销售价格？

参考答案：

【答案】（1）；（2）当销售价格为66元时，利润最大，最大利润为6250元；（3）销售价格控制在55元到70元之间才能使每月利润不少于6000元．

【解析】

试题分析：（1）直接根据题意售价每涨1元每月要少卖10件；售价每下降1元每月要多卖20件，进而得出等量关系；（2）利用每件利润×销量＝总利润，进而利用配方法求出即可；（3）利用函数图象结合一元二次方程的解法得出符合题意的答案．

试题解析：（1）由题意可得，．

（2）由题意可得：，

化简得：，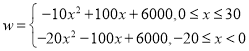

即，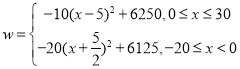

由题意可知应取整数，故当或时，，

故当销售价格为66元时，利润最大，最大利润为6250元.

（3）由题意，如图，令，

即，，

解得：，，，

，

故将销售价格控制在55元到70元之间（含55元和70元）才能使每月利润不少于6000元．

关闭