
分析 先求出基本事件总数$n={C}_{40}^{2}$,再求出恰有1件次品包含的基本事件个数m=${C}_{28}^{1}{C}_{12}^{1}$,由此能求出恰有1件次品的概率.
解答 解:在40件产品中有12件次品,从中任取2件,
基本事件总数$n={C}_{40}^{2}$=780,
恰有1件次品包含的基本事件个数m=${C}_{28}^{1}{C}_{12}^{1}$=336,
则恰有1件次品的概率为p=$\frac{m}{n}=\frac{336}{780}$=$\frac{28}{65}$.
故答案为:$\frac{28}{65}$.
点评 本题考查概率的求法,涉及到古典概型、排列、组合等知识点,考查推理论证能力、运算求解能力、数据处理能力,考查化归与转化思想,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
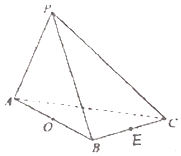 在三棱锥P-ABC中,△PAC和△PBC是边长为$\sqrt{2}$的等边三角形,AB=2,O是AB中点,E是BC中点.
在三棱锥P-ABC中,△PAC和△PBC是边长为$\sqrt{2}$的等边三角形,AB=2,O是AB中点,E是BC中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 20 | C. | 16 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | 3 | C. | $\frac{9}{4}$ | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,我校计划建一个面积为200m2的矩形场地,要求矩形场地的一面利用旧墙(旧墙需要维修),其余三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为41元/米,新墙的造价为400元/米.设利用旧墙的长度为x(单位:米),修建此矩形场地围墙的总费用y(单位:元).
如图,我校计划建一个面积为200m2的矩形场地,要求矩形场地的一面利用旧墙(旧墙需要维修),其余三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为41元/米,新墙的造价为400元/米.设利用旧墙的长度为x(单位:米),修建此矩形场地围墙的总费用y(单位:元).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com