
(本小题满分13分)已知函数f (x)=ln x-a2x2+ax (a∈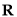 ).
).
(1)当a=1时,求函数f (x)的单调区间;
(2)若函数f (x)在区间 (1,+∞)上是减函数,求实数a的取值范围.
(1)函数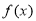 的单调递增区间是
的单调递增区间是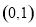 ,单调递减区间是
,单调递减区间是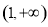 ;
;
(2)实数a的取值范围是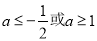 .
.
【解析】
试题分析:(1)当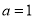 时,
时,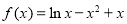 ,定义域是
,定义域是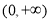 .首先求得:
.首先求得: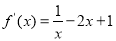 ,再利用导数的符号判断函数
,再利用导数的符号判断函数 的单调性并求单调区间;
的单调性并求单调区间;
(2)首先求出函数 的导数
的导数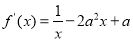 ,因为函数f (x)在区间 (1,+∞)上是减函数,所以所以
,因为函数f (x)在区间 (1,+∞)上是减函数,所以所以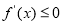 在
在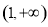 上恒成立;转化为二次函数、二次方程与二次不等式问题.
上恒成立;转化为二次函数、二次方程与二次不等式问题.
试题解析:【解析】
(Ⅰ)当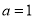 时,
时,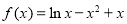 ,定义域是
,定义域是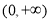 .
.
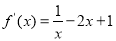 ,
,
由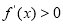 ,解得
,解得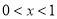 ;由
;由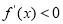 ,解得
,解得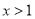 ;
;
所以函数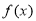 的单调递增区间是
的单调递增区间是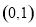 ,单调递减区间是
,单调递减区间是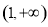 . 5分
. 5分
(2)(法一)
因为函数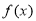 在区间
在区间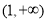 上是减函数,所以
上是减函数,所以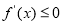 在
在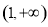 上恒成立,
上恒成立,
则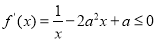 ,即
,即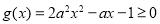 在
在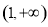 上恒成立. 7分
上恒成立. 7分
当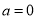 时,
时,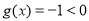 ,所以
,所以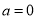 不成立. 9分
不成立. 9分
当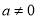 时,
时,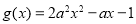 ,
,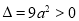 ,对称轴
,对称轴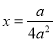 .
.
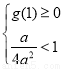 ,即
,即 ,解得
,解得
所以实数a的取值范围是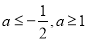 . 13分
. 13分
(法二)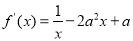
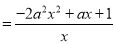 ,定义域是
,定义域是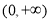 .
.
①当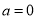 时,
时, 在区间
在区间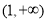 上是增函数,所以
上是增函数,所以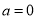 不成立. 8分
不成立. 8分
②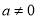 时,
时,
令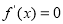 ,即
,即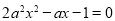 ,则
,则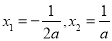 , 9分
, 9分
(1)当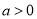 时,由
时,由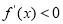 ,解得
,解得 ,
,
所以函数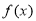 的单调递减区间是
的单调递减区间是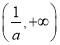 .
.
因为函数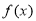 在区间
在区间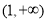 上是减函数,+所以
上是减函数,+所以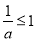 ,解得
,解得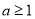 . 11分
. 11分
(2)当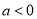 时,由
时,由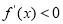 ,解得
,解得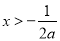 ,
,
所以函数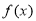 的单调递减区间是
的单调递减区间是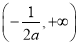 .
.
因为函数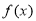 在区间
在区间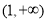 上是减函数,所以
上是减函数,所以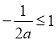 ,解得
,解得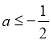 .
.
综上实数a的取值范围是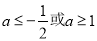 . 13分
. 13分
考点:1、导数在研究函数性质中的应用;2、二次函数、二次方程与一元二次不等式综合问题;3、等价转化的思想与数形结合的思想.


科目:高中数学 来源:2014-2015学年北京市高三上学期期中考试文科数学试卷(解析版) 题型:解答题
(本小题满分13分)已知在等比数列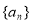 中,
中,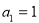 ,且
,且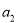 是
是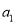 和
和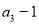 的等差中项.
的等差中项.
(Ⅰ)求数列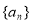 的通项公式;
的通项公式;
(Ⅱ)若数列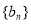 满足
满足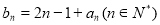 ,求
,求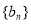 的前
的前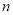 项和
项和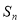 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省厦门市高三上学期期末质量检测理科数学试卷(解析版) 题型:选择题
等差数列 中,
中, 和
和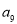 是关于方程
是关于方程 的两根,则该数列的前11项和
的两根,则该数列的前11项和 ( )
( )
A.58 B.88 C.143 D.176
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市昌平区高三上学期期末质量抽测文科数学试卷(解析版) 题型:填空题
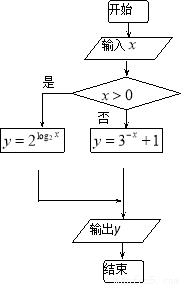
执行如图所示的程序框图,如果输入 ,那么输出的结果是 ,如果输入
,那么输出的结果是 ,如果输入 ,那么输出的结果是 .
,那么输出的结果是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市昌平区高三上学期期末质量抽测理科数学试卷(解析版) 题型:选择题
已知双曲线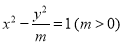 的离心率是2,则
的离心率是2,则 以该双曲线的右焦点为圆心且与其渐近线相切的圆的方程是 .
以该双曲线的右焦点为圆心且与其渐近线相切的圆的方程是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市昌平区高三上学期期末质量抽测理科数学试卷(解析版) 题型:选择题
在2014年APEC会议期间,北京某旅行社为某旅行团包机去旅游,其中旅行社的包机费为12000元,旅行团中每人的飞机票按以下方式与旅行社结算:若旅行团的人数在30人或30人以下,每张机票收费800元;若旅行团的人数多于30人,则给予优惠,每多1人,旅行团每张机票减少20元,但旅行团的人数最多不超过45人,当旅行社获得的机票利润最大时,旅行团的人数是
A. 32人 B.35人 C. 40人 D.45 人
查看答案和解析>>
科目:高中数学 来源:2014-2015学年吉林省高一上学期一模数学试卷(解析版) 题型:选择题
函数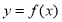 的定义域为[1,5],则函数
的定义域为[1,5],则函数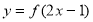 的定义域是( )
的定义域是( )
A.[1,5] B.[2,10] C.[1,9] D.[1,3]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com