
 设X~N(μ1,σ12),Y~N(μ2,σ22),这两个正态分布密度曲线如图所示.下列结论中正确的是( )
设X~N(μ1,σ12),Y~N(μ2,σ22),这两个正态分布密度曲线如图所示.下列结论中正确的是( )| A. | P(Y≥μ2)≥P(Y≥μ1) | B. | P(X≤σ2)≤P(X≤σ1) | ||
| C. | 对任意正数t,P(X≤t)≥P(Y≤t) | D. | 对任意正数t,P(X≥t)≥P(Y≥t) |
科目:高中数学 来源: 题型:选择题
 某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届辽宁庄河市高三9月月考数学(文)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在平面直角坐标系 中,动点
中,动点 的坐标为
的坐标为 ,其中
,其中 .在极坐标系(以原点
.在极坐标系(以原点 为极点,以
为极点,以 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线 的方程为
的方程为 .
.
(Ⅰ)判断动点 的轨迹的形状;
的轨迹的形状;
(Ⅱ)若直线 与动点
与动点 的轨迹有且仅有一个公共点,求实数
的轨迹有且仅有一个公共点,求实数 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2017届辽宁庄河市高三9月月考数学(理)试卷(解析版) 题型:选择题
已知命题 :若
:若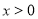 ,则函数
,则函数 的最小值为
的最小值为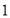 ;命题
;命题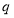 :若
:若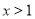 ,则
,则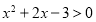 .则
.则
下列命题是真命题的是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com