【题目】已知函数f（x）=2cosxsin（x﹣ 
）+ 
．
（1）求函数f（x）的对称轴方程；
（2）若方程sin2x+2|f（x+ 
）|﹣m+1=0在x∈[﹣ 
， 
]上有三个实数解，求实数m的取值范围．
【答案】
（1）解：f（x）=2cosxsin（x﹣ 
）+ 
= 
sinxcosx﹣ 
= 
=sin（2x﹣ ），
∴函数f（x）的对称轴方程x= 
，k∈Z
（2）解：方程sin2x+2|f（x+ 
）|﹣m+1=0可化为方程sin2x+2|sin2x|=m﹣1．
令g（x）=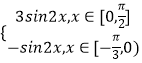 
若方程有三个实数解，则m﹣1=1或0＜m﹣1＜ 
∴m=2或1＜m＜1+
【解析】（1）利用差角的正弦公式、二倍角公式、辅助角公式，化简函数，即可求函数f（x）的对称轴方程；（2）方程sin2x+2|f（x+ ）|﹣m+1=0可化为方程sin2x+2|sin2x|=m﹣1．令g（x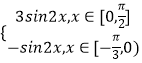）= ，根据方程有三个实数解，则m﹣1=1或0＜m﹣1＜ ，即可求实数m的取值范围．
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=log2（16x+k）﹣2x （k∈R）是偶函数．
（1）求k；
（2）若不等式m﹣1≤f（x）≤2m+log217在x∈[﹣1， 
]上恒成立，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】经市场调查，某商品每吨的价格为x（2＜x＜14）元时，该商品的月供给量为y1吨，y1=ax﹣16（a≥8）；月需求量为y2吨
．当该商品的需求量不小于供给量时，销售量等于供给量；当该商品的需求量小于供给量时，销售量等于需求量．该商品的月销售额f（x）等于月销售量与价格的乘积．
（1）若a=32，问商品的价格为多少元时，该商品的月销售额f（x）最大？
（2）记需求量与供给量相等时的价格为均衡价格．若该商品的均衡价格不低于每吨10元，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（12分）已知函数
．
（1）若x=2是函数f（x）的极值点，求曲线y=f（x）在点（1,f（1））处的切线方程；
（2）若函数f（x）在
上为单调增函数，求a的取值范围；
（3）设m，n为正实数，且m>n，求证： 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知二次函数f（x）=ax2+bx+c．
（1）若a=c＞0，f（1）=1，对任意x∈|[﹣2，2]，f（x）的最大值与最小值之和为g（a），求g（a）的表达式；
（2）若a，b，c为正整数，函数f（x）在（﹣ 
， ）上有两个不同零点，求a+b+c的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列函数f（x）中，满足“对任意x1、x2∈（0，+∞），当x1＜x2时，都有f（x1）＞f（x2）”的是（ ）
A.f（x）=（x﹣1）2
B.f（x）=ex
C.f（x）= 
D.f（x）=ln（x+1）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
