练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若函数f（x）=x2﹣2|x|+m有两个相异零点，则实数m的取值范围是 ．

    【答案】m=1或m＜0
    【解析】解：函数g（x）=x2﹣2|x|的图象，如图所示， ∵函数f（x）=x2﹣2|x|+m有两个相异零点，
    ∴﹣m=﹣1或﹣m＞0，
    ∴m=1或m＜0．
    所以答案是m=1或m＜0．

    【考点精析】解答此题的关键在于理解函数的零点与方程根的关系的相关知识，掌握二次函数的零点：（1）△＞0，方程 有两不等实根，二次函数的图象与 轴有两个交点，二次函数有两个零点;（2）△＝0，方程 有两相等实根（二重根），二次函数的图象与 轴有一个交点，二次函数有一个二重零点或二阶零点;（3）△＜0，方程 无实根，二次函数的图象与 轴无交点，二次函数无零点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=Asin（ωx+θ）（ A＞0，ω＞0，|θ|＜ ）的最小正周期为π，且图象上有一个最低点为M（ ，﹣3）．
    （1）求f（x）的解析式；
    （2）求函数f（x）在[0，π]的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2cosxsin（x﹣ ）+ ．
    （1）求函数f（x）的对称轴方程；
    （2）若方程sin2x+2|f（x+ ）|﹣m+1=0在x∈[﹣ ， ]上有三个实数解，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列四个命题中正确的有
    ①函数y= 的定义域是{x|x≠0}；
    ②lg =lg（x﹣2）的解集为{3}；
    ②31﹣x﹣2=0的解集为{x|x=1﹣log32}；
    ④lg（x﹣1）＜1的解集是{x|x＜11}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=lg（2+x）+lg（2﹣x）．

    （1）求函数f（x）的定义域并判断函数f（x）的奇偶性；

    （2）记函数g（x）= +3x，求函数g（x）的值域；

    （3）若不等式 f（x）＞m有解，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设等比数列的公比为，前项和.

    （1）求的取值范围；

    （2）设，记的前项和为，试比较与的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB＝，AC＝3， BC＝2，P是△ABC内的一点．

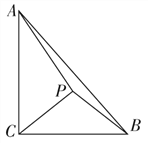
    （1）若P是等腰直角三角形PBC的直角顶点，求PA的长；

    （2）若∠BPC＝，设∠PCB＝θ，求△PBC的面积S(θ)的解析式，并求S(θ)的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x﹣ ．
    （1）用函数单调性的定义证明：函数f（x）在区间（0，+∞）上为增函数；
    （2）方程2tf（4t）﹣mf（2t）=0，当t∈[1，2]时，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ，
    （1）求函数的定义域；
    （2）求 的值．

    查看答案和解析>>

    同步练习册答案