
【题目】已知函数f(x)=x﹣ ![]() .
.
(1)用函数单调性的定义证明:函数f(x)在区间(0,+∞)上为增函数;
(2)方程2tf(4t)﹣mf(2t)=0,当t∈[1,2]时,求实数m的取值范围.
【答案】
(1)证明:设x1,x2∈(0,+∞),且x1<x2,则:
![]() =
= ![]() ;
;
∵x1,x2>0,且x1<x2;
∴x1﹣x2<0, ![]() ;
;
∴f(x1)<f(x2);
∴f(x)在区间(0,+∞)上为增函数
(2)解:根据解析式f(x)=x﹣ ![]() ,原方程变成:
,原方程变成: ![]() ;
;
整理得,(22t)2﹣m22t+m﹣1=0;
∴(22t﹣1)[22t﹣(m﹣1)]=0 ①;
∵t∈[1,2];
∴22t∈[4,16];
∴22t﹣1>0;
∴由方程①得,22t﹣(m﹣1)=0;
∴m﹣1=22t;
∴4≤m﹣1≤16;
∴5≤m≤17;
∴实数m的取值范围为[5,17]
【解析】(1)根据单调性的定义,设x1 , x2∈(0,+∞),且x1<x2 , 然后通过作差证明f(x1)<f(x2)即可;(2)求出f(4t),f(2t),所以原方程可变成(22t)2﹣m2t+m﹣1=0,该方程又可变成(22t﹣1)[22t﹣(m﹣1)]=0,可以得到4≤22t≤16,m﹣1=22t , 所以得到4≤m﹣1≤16,解不等式即得实数m的取值范围.
【考点精析】掌握函数单调性的判断方法是解答本题的根本,需要知道单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】经市场调查,某商品每吨的价格为x(2<x<14)元时,该商品的月供给量为y1吨,y1=ax﹣16(a≥8);月需求量为y2吨![]() .当该商品的需求量不小于供给量时,销售量等于供给量;当该商品的需求量小于供给量时,销售量等于需求量.该商品的月销售额f(x)等于月销售量与价格的乘积.
.当该商品的需求量不小于供给量时,销售量等于供给量;当该商品的需求量小于供给量时,销售量等于需求量.该商品的月销售额f(x)等于月销售量与价格的乘积.
(1)若a=32,问商品的价格为多少元时,该商品的月销售额f(x)最大?
(2)记需求量与供给量相等时的价格为均衡价格.若该商品的均衡价格不低于每吨10元,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列叙述: ①若α,β均为第一象限,且α>β,则sinα>sinβ
②函数f(x)=sin(2x﹣ ![]() )在区间[0,
)在区间[0, ![]() ]上是增函数;
]上是增函数;
③函数f(x)=cos(2x+ ![]() )的一个对称中心为(﹣
)的一个对称中心为(﹣ ![]() ,0)
,0)
④记min{a,b}= ![]() ,若函数f(x)=min{sinx,cosx},则f(x)的值域为[﹣1,
,若函数f(x)=min{sinx,cosx},则f(x)的值域为[﹣1, ![]() ].
].
其是叙述正确的是(请填上序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() +
+ ![]() =1(a>b>0)的右焦点为F2(1,0),点H(2,
=1(a>b>0)的右焦点为F2(1,0),点H(2, ![]() )在椭圆上.
)在椭圆上. 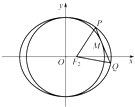
(1)求椭圆的方程;
(2)点M在圆x2+y2=b2上,且M在第一象限,过M作圆x2+y2=b2的切线交椭圆于P,Q两点,问:△PF2Q的周长是否为定值?如果是,求出定值;如果不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.“x<﹣1”是“x2﹣x﹣2>0”的必要不充分条件
B.“P且Q”为假,则P假且 Q假
C.命题“ax2﹣2ax+3>0恒成立”是真命题,则实数a的取值范围是0≤a<3
D.命题“若x2﹣3x+2=0,则x=2”的否命题为“若x2﹣3x+2=0,则x≠2”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数f(x)中,满足“对任意x1、x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2)”的是( )
A.f(x)=(x﹣1)2
B.f(x)=ex
C.f(x)= ![]()
D.f(x)=ln(x+1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com