
分析 (I)若a=0,求函数的导数,利用导数求f(x)的单调区间;
(II)利用导数分别讨论a的取值,进而讨论函数f(x)在区间($\frac{1}{e}$,+∞)上的极值点个数;
(III)假设存在a,使得f(x)在区间($\frac{1}{e}$,+∞)上与x轴相切,则f(x)必与x轴相切于极值点处,利用导数与极值之间的关系进行讨论.
解答 解:(Ⅰ)当a=0时,f(x)=(xlnx-1)ex,(x>0)
导数f′(x)=(x+1)exlnx,
所以x∈(0,1),f′(x)<0;x∈(1,+∞),f′(x)>0.
可得f(x)的减区间为(0,1),f(x)的增区间为(1,+∞);
(Ⅱ)f′(x)=(lnx+xlnx+ax+a2)ex,令m(x)=lnx+xlnx+ax+a2
m′(x)=$\frac{1}{x}$+lnx+1+a,又令φ(x)=$\frac{1}{x}$+lnx+1+a
φ′(x)=-$\frac{1}{{x}^{2}}$+$\frac{1}{x}$.x∈(0,1)时,φ(x)<0,φ(x)递减;
x∈(1,+∞),φ(x)>0,φ(x)递增.
m(x)min=m′(1)=2+a≥0,所以m(x)在区间($\frac{1}{e}$,+∞)单调递增,
m($\frac{1}{e}$)=(a-1)(a+1+$\frac{1}{e}$),
①m($\frac{1}{e}$)≥0,即:-2≤a≤-1-$\frac{1}{e}$或a≥1时m(x)在区间($\frac{1}{e}$,+∞)上无零点,f(x)无极值点
②m($\frac{1}{e}$)<0,即:-1-$\frac{1}{e}$<a<1,m(x)在区间($\frac{1}{e}$,+∞)上有唯一零点,f(x)有唯一极值点.
(Ⅲ)假设存在a,使得f(x)在区间($\frac{1}{e}$,+∞)上与x轴相切,
则f(x)必与x轴相切于极值点.
由(2)可知-1-$\frac{1}{e}$<a<1,设极值点为x0
$\left\{\begin{array}{l}{f′(x)=(ln{x}_{0}+{x}_{0}ln{x}_{0}+a{x}_{0}+{a}^{2}){e}^{{x}_{0}}=0}\\{f(x)=({x}_{0}ln{x}_{0}+a{x}_{0}+{a}^{2}-a-1){e}^{{x}_{0}}=0}\end{array}\right.$,
联立得x0=e-(a+1)代入上式得e-(a+1)+(a+1)-a2=0
令t=-(a+1),t∈(-2,$\frac{1}{e}$),h(t)=et-t-(t+1)2
h′(t)=et-2t-3,h″(t)=et-2<0
h′(t)在t∈(-2,$\frac{1}{e}$)上单调递减,h′(-2)=e-2+1>0,$h′(\frac{1}{e})$<0
∴h′(t)在t∈(-2,$\frac{1}{e}$)上存在唯一零点t0
即当t∈(-2,t0)时,h′(t)>0,h(t)单调递增,当t∈(t0,$\frac{1}{e}$)时,h(t)<0,h(t)单调递减
h(-2)>0,h($\frac{1}{e}$)<0,所以h(t)在t∈(-2,t0)上无零点,在t∈(t0,$\frac{1}{e}$)上有唯一零点
h(0)=0,a+1=0,a=-1
所以存在a=-1,使得f(x)在区间($\frac{1}{e}$,+∞)上与x轴相切.
点评 本题主要考查利用导数研究函数的单调性和极值,综合性较强,运算量较大,考查学生的运算能力,是一道难度非常大的难题.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:选择题
 定义运算a*b为执行如图所示的程序框图输出的S值,则(sin$\frac{5π}{12}}$)*(${cos\frac{5π}{12}}$)的值为( )
定义运算a*b为执行如图所示的程序框图输出的S值,则(sin$\frac{5π}{12}}$)*(${cos\frac{5π}{12}}$)的值为( )| A. | $\frac{{2-\sqrt{3}}}{4}$ | B. | $\frac{{2+\sqrt{3}}}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,0) | C. | (0,$\frac{1}{4}$) | D. | ($\frac{1}{4}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
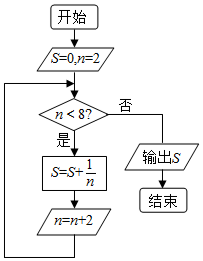 如图所示,执行程序框图,输出结果( )
如图所示,执行程序框图,输出结果( )| A. | $\frac{5}{12}$ | B. | $\frac{7}{12}$ | C. | $\frac{11}{12}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{55}}}{8}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x+3>0\\ x-5<0\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+3<0\\ x-5>0\end{array}\right.$ | C. | $\left\{\begin{array}{l}x-5>0\\ x+3<0\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+3>0\\ x-5>0\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com