
【题目】如图,在四棱锥A﹣BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= ![]() .
. 
(1)证明:DE⊥平面ACD;
(2)求二面角B﹣AD﹣E的大小.
【答案】
(1)证明:在直角梯形BCDE中,由DE=BE=1,CD=2,得BD=BC= ![]() ,
,
由AC= ![]() ,AB=2得AB2=AC2+BC2,即AC⊥BC,
,AB=2得AB2=AC2+BC2,即AC⊥BC,
又平面ABC⊥平面BCDE,从而AC⊥平面BCDE,
所以AC⊥DE,又DE⊥DC,从而DE⊥平面ACD;
(2)解:作BF⊥AD,与AD交于点F,过点F作FG∥DE,与AE交于点G,连接BG,由(Ⅰ)知DE⊥AD,则FG⊥AD,所以∠BFG就是二面角B﹣AD﹣E的平面角,在直角梯形BCDE中,由CD2=BC2+BD2,得BD⊥BC,
又平面ABC⊥平面BCDE,得BD⊥平面ABC,从而BD⊥AB,
由于AC⊥平面BCDE,得AC⊥CD.
在Rt△ACD中,由DC=2,AC= ![]() ,得AD=
,得AD= ![]() ;
;
在Rt△AED中,由ED=1,AD= ![]() 得AE=
得AE= ![]() ;
;
在Rt△ABD中,由BD= ![]() ,AB=2,AD=
,AB=2,AD= ![]() 得BF=
得BF= ![]() ,AF=
,AF= ![]() AD,从而GF=
AD,从而GF= ![]() ,
,
在△ABE,△ABG中,利用余弦定理分别可得cos∠BAE= ![]() ,BG=
,BG= ![]() .
.
在△BFG中,cos∠BFG= ![]() =
= ![]() ,
,
所以,∠BFG= ![]() ,二面角B﹣AD﹣E的大小为
,二面角B﹣AD﹣E的大小为 ![]() .
.

【解析】(1)依题意,易证AC⊥平面BCDE,于是可得AC⊥DE,又DE⊥DC,从而DE⊥平面ACD;(2)作BF⊥AD,与AD交于点F,过点F作FG∥DE,与AE交于点G,连接BG,由(1)知DE⊥AD,则FG⊥AD,所以∠BFG就是二面角B﹣AD﹣E的平面角,利用题中的数据,解三角形,可求得BF= ![]() ,AF=
,AF= ![]() AD,从而GF=
AD,从而GF= ![]() ,cos∠BFG=
,cos∠BFG= ![]() =
= ![]() ,从而可求得答案.
,从而可求得答案.
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某二手车交易市场对某型号的二手汽车的使用年数![]() 与销售价格
与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(1)试求![]() 关于
关于![]() 的回归直线方程:(参考公式:
的回归直线方程:(参考公式: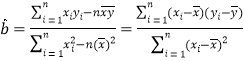 ,
, ![]() .)
.)
(2)已知每辆该型号汽车的收购价格为![]() 万元,根据(1)中所求的回归方程,预测
万元,根据(1)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
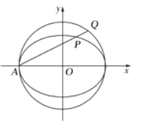
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,长轴长为4,过椭圆的左顶点
,长轴长为4,过椭圆的左顶点![]() 作直线
作直线![]() ,分别交椭圆和圆
,分别交椭圆和圆![]() 于相异两点
于相异两点![]()
(1) 若直线![]() 的斜率为1,求
的斜率为1,求![]() 的值:
的值:
(2) 若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如:
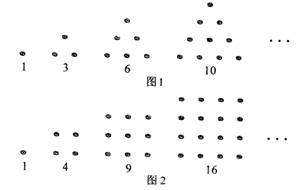
他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是( )
A. 36 B. 45 C. 99 D. 100
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosxsin(x+ ![]() )﹣
)﹣ ![]() cos2x+
cos2x+ ![]() ,x∈R.
,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在闭区间[﹣ ![]() ,
, ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】身体素质拓展训练中,人从竖直墙壁的顶点A沿光滑杆自由下滑到倾斜的木板上(人可看作质点),若木板的倾斜角不同,人沿着三条不同路径AB、AC、AD滑到木板上的时间分别为t1、t2、t3,若已知AB、AC、AD与板的夹角分别为70o、90o和105o,则( )

A. t1>t2>t3 B. t1<t2<t3 C. t1=t2=t3 D. 不能确定t1、t2、t3之间的关系
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com