(1)a
n+24=a
n;所以a
2010=a
18(2分)
a
18是以

为首项,以

为公比的等比数列的第6项,
所以
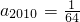
(4分)
(2)

,所以m≥7(5分)
因为
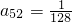
,所以2km+m+7=(2k+1)m+7=52,其中m≥7,m∈N,k∈N(6分)
(2k+1)m=45,
当k=0时,m=45,成立.
当k=1时,m=15,成立;
当k=2时,m=9成立(9分)
当k≥3时,
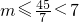
;
所以m可取9、15、45(10分)
(3)
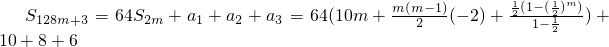
(12分)
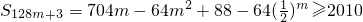
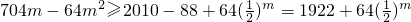
设f(m)=704m-64m
2,
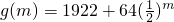
(14分)
g(m)>1922;
f(m)=-64(m
2-11m),对称轴

,
所以f(m)在m=5或6时取最大f(x)
max=f(5)=f(6)=1920,
因为1922>1920,所以不存在这样的m(16分)
分析:(1)由a
n+24=a
n,知a
2010=a
18,a
18是以

为首项,以

为公比的等比数列的第6项,所以
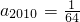
.
(2)由

,知m≥7,由
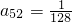
,知2km+m+7=(2k+1)m+7=52,由此入手可求出m可取9、15、45.
(3)由
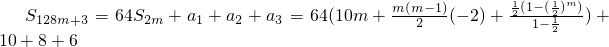
,知
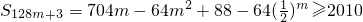
,
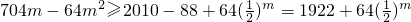
.设f(m)=704m-64m
2,
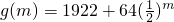
>1922;f(m)=-64(m
2-11m),f(x)
max=f(5)=f(6)=1920,所以不存在这样的m.
点评:本题考查数列的不等式的综合应用,解题时要认真审题,注意计算能力的培养.

 ,公比为
,公比为 的等比数列(m≥3,m∈N*),并对任意n∈N*,均有an+2m=an成立.
的等比数列(m≥3,m∈N*),并对任意n∈N*,均有an+2m=an成立.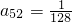 ,试求m的值;
,试求m的值; 为首项,以
为首项,以 为公比的等比数列的第6项,
为公比的等比数列的第6项,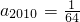 (4分)
(4分) ,所以m≥7(5分)
,所以m≥7(5分)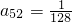 ,所以2km+m+7=(2k+1)m+7=52,其中m≥7,m∈N,k∈N(6分)
,所以2km+m+7=(2k+1)m+7=52,其中m≥7,m∈N,k∈N(6分)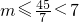 ;
;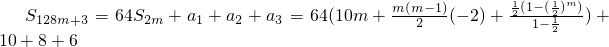 (12分)
(12分)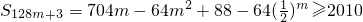
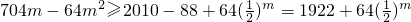
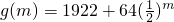 (14分)
(14分) ,
, 为首项,以
为首项,以 为公比的等比数列的第6项,所以
为公比的等比数列的第6项,所以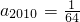 .
. ,知m≥7,由
,知m≥7,由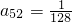 ,知2km+m+7=(2k+1)m+7=52,由此入手可求出m可取9、15、45.
,知2km+m+7=(2k+1)m+7=52,由此入手可求出m可取9、15、45.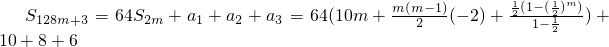 ,知
,知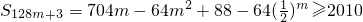 ,
,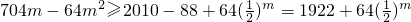 .设f(m)=704m-64m2,
.设f(m)=704m-64m2,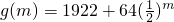 >1922;f(m)=-64(m2-11m),f(x)max=f(5)=f(6)=1920,所以不存在这样的m.
>1922;f(m)=-64(m2-11m),f(x)max=f(5)=f(6)=1920,所以不存在这样的m.
