
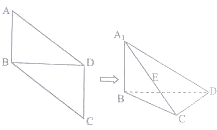
 如图,在平行四边形ABCD中,AB=1,BD=$\sqrt{2}$,∠ABD=90°,将△ABD沿对角线BD折起,折后的点A变为A1,且A1C=2.
如图,在平行四边形ABCD中,AB=1,BD=$\sqrt{2}$,∠ABD=90°,将△ABD沿对角线BD折起,折后的点A变为A1,且A1C=2.分析 (1)对比折叠前后即可得到${A}_{1}B=1,BC=\sqrt{3}$,并且A1C=2,从而得到A1B⊥BC,并且A1B⊥BD,从而得到A1B⊥平面BCD,根据面面垂直的判定定理即可得出平面A1BD⊥平面BCD;
(2)在平面BCD内,过B作BD的垂线,从而可以BD的垂线,BD,BA1三直线分别为x,y,z轴,建立空间直角坐标系,求出图形上各点的坐标,从而求出向量$\overrightarrow{BC}$,$\overrightarrow{{A}_{1}D}$的坐标,从而求出cos$<\overrightarrow{BC},\overrightarrow{{A}_{1}D}>$,从而得出异面直线BC与A1D所成角的余弦值;
(3)根据折叠后图形各边的长度设E(x,$\sqrt{2}x,1-x$),从而写出$\overrightarrow{DE}$的坐标,$\overrightarrow{B{A}_{1}}$为平面BCD的一条法向量,并且DE与平面BCD所成的角正弦值为$\frac{\sqrt{7}}{7}$,从而根据$|cos<\overrightarrow{B{A}_{1}},\overrightarrow{DE}>|=\frac{\sqrt{7}}{7}$即可求出x,从而求出EC的长.
解答 解:(1)根据已知条件,在△A1BC中,BC=$\sqrt{3}$,A1B=1,A1C=2;
∴${A}_{1}{B}^{2}+B{C}^{2}={A}_{1}{C}^{2}$;
∴A1B⊥BC;
又A1B⊥BD,BD∩BC=B;
∴A1B⊥平面BCD,A1B?平面A1BD;
∴平面A1BD⊥平面BCD;
(2)以BD的垂线,BD,BA1三直线分别为x,y,z轴,建立如图所示空间直角坐标系,则: B(0,0,0),C(1,$\sqrt{2}$,0),D(0,$\sqrt{2}$,0),A1(0,0,1);
B(0,0,0),C(1,$\sqrt{2}$,0),D(0,$\sqrt{2}$,0),A1(0,0,1);
∴$\overrightarrow{BC}=(1,\sqrt{2},0)$,$\overrightarrow{{A}_{1}D}=(0,\sqrt{2},-1)$;
∴$cos<\overrightarrow{BC},\overrightarrow{{A}_{1}D}>=\frac{2}{\sqrt{3}×\sqrt{3}}=\frac{2}{3}$;
∴异面直线BC与A1D所成角的余弦值为$\frac{2}{3}$;
(3)$\overrightarrow{B{A}_{1}}=(0,0,1)$为平面BCD的一条法向量,E在线段A1C上;
∴设E(x,$\sqrt{2}$x,1-x),x∈[0,1];
∴$\overrightarrow{DE}=(x,\sqrt{2}(x-1),1-x)$;
∵DE与平面BCD所成的角正弦值为$\frac{\sqrt{7}}{7}$;
∴$|cos<\overrightarrow{DE},\overrightarrow{B{A}_{1}}>|=\frac{1-x}{\sqrt{{x}^{2}+3(x-1)^{2}}}$=$\frac{\sqrt{7}}{7}$;
解得x=$\frac{2}{3}$,或2(舍去);
∴$EC=\frac{\sqrt{7}}{3}$;
即当线段EC=$\frac{\sqrt{7}}{3}$时,DE与平面BCD所成的角正弦值为$\frac{\sqrt{7}}{7}$.
点评 考查直角三角形边的关系,弄清折叠前后图形的对应关系,线面垂直、面面垂直的判定定理,建立空间直角坐标系,利用空间向量求异面直线所成角,以及解决线面角问题的方法,能求空间点的坐标,线面角和平面法向量和直线方向向量夹角的关系,向量夹角余弦的坐标公式.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{3}$,则PC与平面PAD所成角的大小为45°.
如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{3}$,则PC与平面PAD所成角的大小为45°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{\sqrt{e}}$) | B. | (-$\sqrt{e}$,$\frac{1}{\sqrt{e}}$) | C. | (-$\frac{1}{\sqrt{e}}$,$\sqrt{e}$) | D. | (0,$\sqrt{e}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com