解:f′(x)=1+asinx,
(I)当a=-2时,f′(x)=1-2sinx,当f′(x)=0时,x=

.
当x∈(
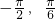
)时,f′(x)>0时,当x∈(
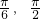
)时,f′(x)<0时,
∴故当x=

时,f(x)有极大值,其极大值为f(

)=

+

.(6分)
(II)当x∈(

)时,|sinx|<1,
(1)当|a|≤1时,得|asinx|<1,此时,f′(x)>0恒成立,没有极值;
(2)当a>1时,得-a<asinx<a,此时,f′(x)=0即1+asinx=0有解,设为α,
由于y=asinx单调增,所以当x∈(-

)时,f′(x)<0,x∈(

)时,f′(x)>0,
∴f(x)在x∈(

)没有极大值;
(3)当a<-1时,得a<asinx<-a,此时,f′(x)=0即1+asinx=0有解,设为β,
由于y=asinx单调增,所以当x∈(-

)时,f′(x)>0,x∈(

)时,f′(x)<0,
∴f(x)在x∈(

)有极大值;
综上所述,f(x)有极大值,实数a的取值范围(-∞,-1)
分析:(1)先求f′(x)=0的值,再分别判定在f′(x)=0的点附近的导数的符号的变化情况,来确定极大值点与极小值点,求出极值.
(2)对字母a进行分类讨论:当|a|≤1时,f′(x)>0恒成立,没有极值;当a>1时,由于y=asinx单调增,f(x)在x∈(

)没有极大值;当a<-1时,得a<asinx<-a,此时,f(x)在x∈(

)有极大值.
点评:本题综合考查了函数的导数的运用及利用导数研究函数的极值,体现了分类讨论的思想在解题中的应用.

 ).
). .
.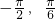 )时,f′(x)>0时,当x∈(
)时,f′(x)>0时,当x∈(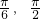 )时,f′(x)<0时,
)时,f′(x)<0时, 时,f(x)有极大值,其极大值为f(
时,f(x)有极大值,其极大值为f( )=
)= +
+ .(6分)
.(6分) )时,|sinx|<1,
)时,|sinx|<1, )时,f′(x)<0,x∈(
)时,f′(x)<0,x∈( )时,f′(x)>0,
)时,f′(x)>0, )没有极大值;
)没有极大值; )时,f′(x)>0,x∈(
)时,f′(x)>0,x∈( )时,f′(x)<0,
)时,f′(x)<0, )有极大值;
)有极大值; )没有极大值;当a<-1时,得a<asinx<-a,此时,f(x)在x∈(
)没有极大值;当a<-1时,得a<asinx<-a,此时,f(x)在x∈( )有极大值.
)有极大值.

 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<