
ЁОЬтФПЁПШчЭМЃЌЖЈвхЃКвдЭждВжааФЮЊдВаФЃЌГЄжсЮЊжБОЖЕФдВНазіЭждВЕФЁАИЈжњдВЁБ.Й§ЭждВЕкЫФЯѓЯоФквЛЕуMзїxжсЕФДЙЯпНЛЦфЁАИЈжњдВЁБгкЕуNЃЌЕБЕуNдкЕуMЕФЯТЗНЪБЃЌГЦЕуNЮЊЕуMЕФЁАЯТИЈжњЕуЁБ.вбжЊЭждВEЃК![]() ЩЯЕФЕу
ЩЯЕФЕу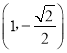 ЕФЯТИЈжњЕуЮЊЃЈ1ЃЌЉ1ЃЉ.
ЕФЯТИЈжњЕуЮЊЃЈ1ЃЌЉ1ЃЉ.
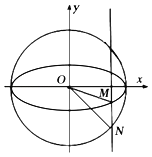
ЃЈ1ЃЉЧѓЭждВEЕФЗНГЬЃЛ
ЃЈ2ЃЉШєЁїOMNЕФУцЛ§ЕШгк![]() ЃЌЧѓЯТИЈжњЕуNЕФзјБъЃЛ
ЃЌЧѓЯТИЈжњЕуNЕФзјБъЃЛ
ЃЈ3ЃЉвбжЊжБЯпlЃКxЉmyЉtЃН0гыЭждВEНЛгкВЛЭЌЕФAЃЌBСНЕуЃЌШєЭждВEЩЯДцдкЕуPЃЌТњзу![]() ЃЌЧѓжБЯпlгызјБъжсЮЇГЩЕФШ§НЧаЮУцЛ§ЕФзюаЁжЕ.
ЃЌЧѓжБЯпlгызјБъжсЮЇГЩЕФШ§НЧаЮУцЛ§ЕФзюаЁжЕ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ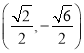 Лђ
Лђ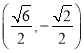 ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉжБНгИљОнЖЈвхЯШЧѓЕУaЃЌНјЖјЕУЕНbМДПЩЃЛ
ЃЈ2ЃЉЩшЕуNЃЈx0ЃЌy0ЃЉЃЈy0ЃМ1ЃЉЃЌдђЕуMЃЈx0ЃЌy1ЃЉЃЈy1ЃМ0ЃЉЃЌИљОнЭждВЗНГЬвдМАУцЛ§ПЩЕУx0y1![]() ЃЌНЋЦфгы
ЃЌНЋЦфгы![]() СЊСЂЕУЕНNзјБъЃЛ
СЊСЂЕУЕНNзјБъЃЛ
ЃЈ3ЃЉЩшAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЌСЊСЂ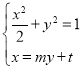 ЃЌНсКЯЮЄДяЖЈРэЕУ
ЃЌНсКЯЮЄДяЖЈРэЕУ ЃЌвђЮЊ
ЃЌвђЮЊ![]() ЧвPдкЭждВЩЯПЩЕУ4t2ЃНm2+2ЃЌБэЪОГіШ§НЧаЮУцЛ§НсКЯЛљБОВЛЕШЪНМДПЩЧѓЦфзюаЁжЕ.
ЧвPдкЭждВЩЯПЩЕУ4t2ЃНm2+2ЃЌБэЪОГіШ§НЧаЮУцЛ§НсКЯЛљБОВЛЕШЪНМДПЩЧѓЦфзюаЁжЕ.
НтЃКЃЈ1ЃЉЁпЭждВ![]() ЩЯЕФЕуЃЈ1ЃЌ
ЩЯЕФЕуЃЈ1ЃЌ![]() ЃЉЕФЯТИЈжњЕуЮЊЃЈ1ЃЌЉ1ЃЉЃЌ
ЃЉЕФЯТИЈжњЕуЮЊЃЈ1ЃЌЉ1ЃЉЃЌ
ЁрИЈжњдВЕФАыОЖЮЊR![]() ЃЌЭждВГЄАыжсЮЊaЃНR
ЃЌЭждВГЄАыжсЮЊaЃНR![]() ЃЌ
ЃЌ
НЋЕуЃЈ1ЃЌ![]() ЃЉДњШыЭждВЗНГЬ
ЃЉДњШыЭждВЗНГЬ![]() жаЃЌНтЕУbЃН1ЃЌ
жаЃЌНтЕУbЃН1ЃЌ
ЁрЭждВEЕФЗНГЬЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩшЕуNЃЈx0ЃЌy0ЃЉЃЈy0ЃМ1ЃЉЃЌдђЕуMЃЈx0ЃЌy1ЃЉЃЈy1ЃМ0ЃЉЃЌНЋСНЕузјБъЗжБ№ДњШыИЈжњдВЗНГЬКЭЭждВЗНГЬПЩЕУЃЌ
x02+y02ЃН2ЃЌ![]() ЃЌЙЪy02ЃН2y12ЃЌМДy0
ЃЌЙЪy02ЃН2y12ЃЌМДy0![]() y1ЃЌ
y1ЃЌ
гжSЁїOMN![]() x0ЃЈy1Љy0ЃЉ
x0ЃЈy1Љy0ЃЉ![]() ЃЌдђx0y1
ЃЌдђx0y1![]() ЃЌ
ЃЌ
НЋx0y1![]() гы
гы![]() СЊСЂПЩНтЕУ
СЊСЂПЩНтЕУ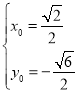 Лђ
Лђ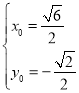 ЃЌ
ЃЌ
ЁрЯТИЈжњЕуNЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉгЩЬтвтПЩЩшAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉ.
СЊСЂ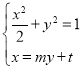 ећРэЕУЃЈm2+2ЃЉy2+2mty+t2Љ2ЃН0ЃЌдђЁїЃН8ЃЈm2+2Љt2ЃЉЃО0.
ећРэЕУЃЈm2+2ЃЉy2+2mty+t2Љ2ЃН0ЃЌдђЁїЃН8ЃЈm2+2Љt2ЃЉЃО0.
ИљОнЮЄДяЖЈРэЕУ ЃЌ
ЃЌ
вђЮЊ![]() .
.
Ыљвд![]() ЃЌ
ЃЌ![]()
вђЮЊЕуPдкЭждВEЩЯЃЌ
Ыљвд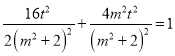 ЃЌ
ЃЌ
ећРэЕУ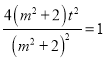 ЃЌ
ЃЌ
МД4t2ЃНm2+2ЃЌ
дкжБЯпlЃКxЉmyЉtЃН0жаЃЌ
гЩгкжБЯпlгызјБъжсЮЇГЩШ§НЧаЮЃЌдђtЁй0ЃЌmЁй0.
СюxЃН0ЃЌЕУ![]() ЃЌСюyЃН0ЃЌЕУxЃНt.
ЃЌСюyЃН0ЃЌЕУxЃНt.
ЫљвдШ§НЧаЮУцЛ§ЮЊ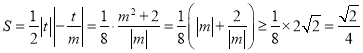 ,
,
ЕБЧвНіЕБm2ЃН2ЃЌt2ЃН1ЪБЃЌШЁЕШКХЃЌДЫЪБЁїЃН24ЃО0.
ЫљвджБЯпlгызјБъжсЮЇГЩЕФШ§НЧаЮУцЛ§ЕФзюаЁжЕЮЊ![]() .
.


 гІгУЬтЬьЬьСЗЫФДЈДѓбЇГіАцЩчЯЕСаД№АИ
гІгУЬтЬьЬьСЗЫФДЈДѓбЇГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈЂёЃЉШєКЏЪ§![]() гаСНИіСуЕуЃЌЧѓaЕФШЁжЕЗЖЮЇЃЛ
гаСНИіСуЕуЃЌЧѓaЕФШЁжЕЗЖЮЇЃЛ
ЃЈЂђЃЉ![]() КуГЩСЂЃЌЧѓaЕФШЁжЕЗЖЮЇ.
КуГЩСЂЃЌЧѓaЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭМ1ЪЧгЩ![]() КЭ
КЭ![]() зщГЩЕФвЛИіЦНУцЭМаЮЃЌЦфжа
зщГЩЕФвЛИіЦНУцЭМаЮЃЌЦфжа![]() ЪЧ
ЪЧ![]() ЕФИпЃЌ
ЕФИпЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌНЋ
ЃЌНЋ![]() КЭ
КЭ![]() ЗжБ№бизХ
ЗжБ№бизХ![]() ЃЌ
ЃЌ![]() елЦ№ЃЌЪЙЕУ
елЦ№ЃЌЪЙЕУ![]() гы
гы![]() жиКЯгкЕуBЃЌGЮЊ
жиКЯгкЕуBЃЌGЮЊ![]() ЕФжаЕуЃЌШчЭМ2.
ЕФжаЕуЃЌШчЭМ2.
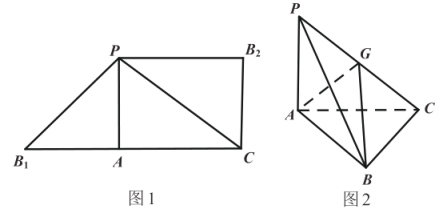
ЃЈ1ЃЉЧѓжЄЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓЕуCЕНЦНУц
ЃЌЧѓЕуCЕНЦНУц![]() ЕФОрРы.
ЕФОрРы.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЧњЯпCЕФВЮЪ§ЗНГЬЮЊ![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌxжсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌжБЯпlЕФМЋзјБъЗНГЬЮЊ
ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌxжсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌжБЯпlЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓЧњЯпCЕФМЋзјБъЗНГЬКЭжБЯпlЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉШєЩфЯп![]() гыЧњЯпCНЛгкЕуAЃЈВЛЭЌгкМЋЕуOЃЉЃЌгыжБЯпlНЛгкЕуBЃЌЧѓ
гыЧњЯпCНЛгкЕуAЃЈВЛЭЌгкМЋЕуOЃЉЃЌгыжБЯпlНЛгкЕуBЃЌЧѓ![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЮЦбљЁБЪЧжаЙњвеЪѕБІПтЕФЙхБІЃЌЁАЛ№ЮЦЁБЪЧГЃМћЕФвЛжжДЋЭГЮЦбљЃЌЮЊСЫВтЫуФГЛ№ЮЦЮЦбљЃЈШчЭМвѕгАВПЗжЫљЪОЃЉЕФУцЛ§ЃЌзївЛИіБпГЄЮЊ3ЕФе§ЗНаЮНЋЦфАќКЌдкФкЃЌВЂЯђИУе§ЗНаЮФкЫцЛњЭЖжР2000ИіЕуЃЌМКжЊЧЁга800ИіЕуТфдквѕгАВПЗжЃЌОнДЫПЩЙРМЦвѕгАВПЗжЕФУцЛ§ЪЧ

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЏКЯ![]() ЃЌ
ЃЌ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌШє
ЃЌШє![]() жагаЧвНігавЛИідЊЫиЃЌдђrЕФжЕЪЧ______.
жагаЧвНігавЛИідЊЫиЃЌдђrЕФжЕЪЧ______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаШЫЭцжРгВБвзпЬјЦхЕФгЮЯЗЃЌвбжЊгВБвГіЯже§ЗДУцЮЊЕШПЩФмадЪТМўЃЌЦхХЬЩЯБъгаЕк0еОЃЌЕк1еОЃЌЕк2еОЃЌЁЁЃЌЕк100еО.вЛУЖЦхзгПЊЪМдкЕк0еОЃЌЦхЪжУПжРвЛДЮгВБвЃЌЦхзгЯђЧАЬјЖЏвЛДЮЃЌШєжРГіе§УцЃЌЦхЯђЧАЬјвЛеОЃЈДгkЕН![]() ЃЉЃЌШєжРГіЗДУцЃЌЦхЯђЧАЬјСНеОЃЈДгkЕН
ЃЉЃЌШєжРГіЗДУцЃЌЦхЯђЧАЬјСНеОЃЈДгkЕН![]() ЃЉЃЌжБЕНЦхзгЬјЕНЕк99еОЃЈЪЄРћДѓБОгЊЃЉЛђЬјЕНЕк100еОЃЈЪЇАмМЏжагЊЃЉЪБЃЌИУгЮЯЗНсЪј.ЩшЦхзгЬјЕНЕкnеОИХТЪЮЊ
ЃЉЃЌжБЕНЦхзгЬјЕНЕк99еОЃЈЪЄРћДѓБОгЊЃЉЛђЬјЕНЕк100еОЃЈЪЇАмМЏжагЊЃЉЪБЃЌИУгЮЯЗНсЪј.ЩшЦхзгЬјЕНЕкnеОИХТЪЮЊ![]() .
.
ЃЈ1ЃЉЧѓ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЧѓ![]() МА
МА![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшМзЁЂввЁЂБћШ§ЬЈЛњЦїЪЧЗёашвЊееЙЫЯрЛЅжЎМфУЛгагАЯьЃЎвбжЊдкФГ1 hФкЃЌМзЁЂввЖМашвЊееЙЫЕФИХТЪЮЊ0.05ЃЌМзЁЂБћЖМашвЊееЙЫЕФИХТЪЮЊ0.1ЃЌввЁЂБћЖМашвЊееЙЫЕФИХТЪЮЊ0.125ЃЎ
ЃЈ1ЃЉЧѓМзЁЂввЁЂБћУПЬЈЛњЦїдкет1 hФкашвЊееЙЫЕФИХТЪЗжБ№ЪЧЖрЩйЃП
ЃЈ2ЃЉМЦЫует1 hФкжСЩйгавЛЬЈЛњЦїашвЊееЙЫЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫФЮЛЭЌбЇВЮМгШ§ЯюВЛЭЌЕФОКШќ.
ЃЈ1ЃЉУПЮЛЭЌбЇБиаыВЮМгвЛЯюЃЌгаМИжжВЛЭЌНсЙћЃП
ЃЈ2ЃЉУПЯюОКШќжЛгаЧвБиаыгавЛЮЛЭЌбЇВЮМгЃЌгаМИжжВЛЭЌНсЙћЃП
ЃЈ3ЃЉУПЮЛЭЌбЇзюЖрВЮМгвЛЯюЃЌЧвУПЯюОКШќжЛаэгавЛЮЛЭЌбЇВЮМгЃЌгаМИжжВЛЭЌНсЙћЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com