
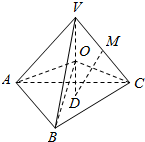
 如图所示,正四面体V-ABC的高VD的中点为O,VC的中点为M.
如图所示,正四面体V-ABC的高VD的中点为O,VC的中点为M.分析 (1)分别设$\overrightarrow{VA}=\overrightarrow{a},\overrightarrow{VB}=\overrightarrow{b},\overrightarrow{VC}=\overrightarrow{c}$,正四面体的棱长为1,把向量$\overrightarrow{AO}、\overrightarrow{BO}、\overrightarrow{CO}$用$\overrightarrow{a}、\overrightarrow{b}、\overrightarrow{c}$表示,然后利用数量积为0证得答案;
(2)由数量积求夹角公式求得<$\overrightarrow{DM},\overrightarrow{AO}$>.
解答 (1)设$\overrightarrow{VA}=\overrightarrow{a},\overrightarrow{VB}=\overrightarrow{b},\overrightarrow{VC}=\overrightarrow{c}$,正四面体的棱长为1,
则$\overrightarrow{VD}=\frac{1}{3}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})$,$\overrightarrow{AO}=\frac{1}{6}(\overrightarrow{b}+\overrightarrow{c}-5\overrightarrow{a})$,
$\overrightarrow{BO}=\frac{1}{6}(\overrightarrow{a}+\overrightarrow{c}-5\overrightarrow{b})$,$\overrightarrow{CO}=\frac{1}{6}(\overrightarrow{a}+\overrightarrow{b}-5\overrightarrow{c})$,
∴$\overrightarrow{AO}•\overrightarrow{BO}=\frac{1}{36}(\overrightarrow{b}+\overrightarrow{c}-5\overrightarrow{a})•(\overrightarrow{a}+\overrightarrow{c}-5\overrightarrow{b})$
=$\frac{1}{36}$(18$\overrightarrow{a}•\overrightarrow{b}-9|\overrightarrow{a}{|}^{2}$)
=$\frac{1}{36}$(18×1×1•cos60°-9)=0.
∴$\overrightarrow{AO}$⊥$\overrightarrow{BO}$,∴AO⊥BO,
同理AO⊥CO,BO⊥CO,
∴AO、BO、CO两两垂直;
(2)$\overrightarrow{DM}=\overrightarrow{DV}+\overrightarrow{VM}$=-$\frac{1}{3}$($\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$)+$\frac{1}{2}\overrightarrow{c}$
=$\frac{1}{6}(-2\overrightarrow{a}-2\overrightarrow{b}+\overrightarrow{c})$.
∴|$\overrightarrow{DM}$|=$\sqrt{[\frac{1}{6}(-2\overrightarrow{a}-2\overrightarrow{b}+\overrightarrow{c})]^{2}}=\frac{1}{2}$,
|$\overrightarrow{AO}$|=$\sqrt{[\frac{1}{6}(\overrightarrow{b}+\overrightarrow{c}-\overrightarrow{a})]^{2}}=\frac{\sqrt{2}}{2}$,
$\overrightarrow{DM}•\overrightarrow{AO}=\frac{1}{6}$=$\frac{1}{6}$($-2\overrightarrow{a}-2\overrightarrow{b}+\overrightarrow{c}$)•$\frac{1}{6}$($\overrightarrow{b}+\overrightarrow{c}-5\overrightarrow{a}$)=$\frac{1}{4}$,
∴cos<$\overrightarrow{DM},\overrightarrow{AO}$>=$\frac{\frac{1}{4}}{\frac{1}{2}•\frac{\sqrt{2}}{2}}=\frac{\sqrt{2}}{2}$,
∵<$\overrightarrow{DM},\overrightarrow{AO}$>∈(0,π),∴<$\overrightarrow{DM},\overrightarrow{AO}$>=$\frac{π}{4}$.
点评 本题考查利用平面向量数量积证明线和线的垂直问题,考查了向量加法的三角形法则,训练了利用向量数量积求向量的夹角,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com