
【题目】
已知函数f(x)=2x3-3(a+1)x2+6ax,a∈R.
(Ⅰ)曲线y=f(x)在x=0处的切线的斜率为3,求a的值;
(Ⅱ)若对于任意x∈(0,+∞),f(x)+f(-x)≥12lnx恒成立,求a的取值范围;
(Ⅲ)若a>1,设函数f(x)在区间[1,2]上的最大值、最小值分别为M(a)、m(a),
记h(a)=M(a)-m(a),求h(a)的最小值.
【答案】(1)![]() (2)(-∞,-1-
(2)(-∞,-1-![]() ](3)
](3)![]()
【解析】试题分析:(1)求出![]() ,由
,由![]() 可得结果;(2)对于任意
可得结果;(2)对于任意![]() 恒成立等价于
恒成立等价于![]() ,利用导数研究函数的单调性,求得
,利用导数研究函数的单调性,求得![]() ,从而可得结果;(3)分三种情况讨论:①当
,从而可得结果;(3)分三种情况讨论:①当![]() ,②当
,②当![]() ,③当
,③当![]() 分别求出
分别求出![]() 的最小值,再比较大小即可得结果.
的最小值,再比较大小即可得结果.
试题解析:(1)因为f(x)=2x3-3(a+1)x2+6ax,所以f ′(x)=6x2-6(a+1)x+6a,
所以曲线y=f(x)在x=0处的切线斜率k=f ′(0)=6a,
所以6a=3,所以a=![]() .
.
(2)f(x)+f(-x)=-6(a+1)x2≥12lnx对任意x∈(0,+∞)恒成立,
所以-(a+1)≥![]() .
.
令g(x)=![]() ,x>0,则g(x)=
,x>0,则g(x)=![]() .
.
令g(x)=0,解得x=![]() .
.
当x∈(0,![]() )时,g(x)>0,所以g(x)在(0,
)时,g(x)>0,所以g(x)在(0,![]() )上单调递增;
)上单调递增;
当x∈(![]() ,+∞)时,g(x)<0,所以g(x)在(
,+∞)时,g(x)<0,所以g(x)在(![]() ,+∞)上单调递减.
,+∞)上单调递减.
所以g(x)max=g(![]() )=
)=![]() ,
,
所以-(a+1)≥![]() ,即a≤-1-
,即a≤-1-![]() ,
,
所以a的取值范围为(-∞,-1-![]() ].
].
(3)因为f(x)=2x3-3(a+1)x2+6ax,
所以f ′(x)=6x2-6(a+1)x+6a=6(x-1)(x-a),f(1)=3a-1,f(2)=4.
令f ′(x)=0,则x=1或a.
f(1)=3a-1,f(2)=4.
①当1<a≤![]() 时,
时,
当x∈(1,a)时,f (x)<0,所以f(x)在(1,a)上单调递减;
当x∈(a,2)时,f (x)>0,所以f(x)在(a,2)上单调递增.
又因为f(1)≤f(2),所以M(a)=f(2)=4,m(a)=f(a)=-a3+3a2,
所以h(a)=M(a)-m(a)=4-(-a3+3a2)=a3-3a2+4.
因为h (a)=3a2-6a=3a(a-2)<0,
所以h(a)在(1,![]() ]上单调递减,
]上单调递减,
所以当a∈(1,![]() ]时,h(a)最小值为h(
]时,h(a)最小值为h(![]() )=
)=![]() .
.
②当![]() <a<2时,
<a<2时,
当x∈(1,a)时,f (x)<0,所以f(x)在(1,a)上单调递减;
当x∈(a,2)时,f (x)>0,所以f(x)在(a,2)上单调递增.
又因为f(1)>f(2),所以M(a)=f(1)=3a-1,m(a)=f(a)=-a3+3a2,
所以h(a)=M(a)-m(a)=3a-1-(-a3+3a2)=a3-3a2+3a-1.
因为h (a)=3a2-6a+3=3(a-1)2≥0.
所以h(a)在( ,2)上单调递增,
,2)上单调递增,
所以当a∈(![]() ,2)时,h(a)>h(
,2)时,h(a)>h(![]() )=
)=![]() .
.
③当a≥2时,
当x∈(1,2)时,f (x)<0,所以f(x)在(1,2)上单调递减,
所以M(a)=f(1)=3a-1,m(a)=f(2)=4,
所以h(a)=M(a)-m(a)=3a-1-4=3a-5,
所以h(a)在[2,+∞)上的最小值为h(2)=1.
综上,h(a)的最小值为![]() .
.
【方法点晴】本题主要考查导数的几何意义、利用导数求函数的最值以及不等式恒成立问题,属于难题.不等式恒成立问题常见方法:① 分离参数![]() 恒成立(
恒成立(![]() 可)或
可)或![]() 恒成立(
恒成立(![]() 即可);② 数形结合(
即可);② 数形结合(![]() 图象在
图象在![]() 上方即可);③ 讨论最值
上方即可);③ 讨论最值![]() 或
或![]() 恒成立;④ 讨论参数.
恒成立;④ 讨论参数.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设点![]() 是
是![]() 轴上的一个定点,其横坐标为
轴上的一个定点,其横坐标为![]() (
(![]() ),已知当
),已知当![]() 时,动圆
时,动圆![]() 过点
过点![]() 且与直线
且与直线![]() 相切,记动圆
相切,记动圆![]() 的圆心
的圆心![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)当![]() 时,若直线
时,若直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() (
(![]() ),且
),且![]() 与以定点
与以定点![]() 为圆心的动圆
为圆心的动圆![]() 也相切,当动圆
也相切,当动圆![]() 的面积最小时,证明:
的面积最小时,证明: ![]() 、
、![]() 两点的横坐标之差为定值.
两点的横坐标之差为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
(1)函数f(x)在x>0时是增函数,x<0时也是增函数,所以f(x)是增函数;
(2)若m=loga2,n=logb2且m>n,则a<b;
(3)函数f(x)=x2+2(a﹣1)x+2在区间(﹣∞,4]上是减函数,则实数a的取值范围是a≤﹣3;
(4)y=log ![]() (x2+x﹣2)的减区间为(1,+∞).
(x2+x﹣2)的减区间为(1,+∞).
其中正确的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在半径为3m的 ![]() 圆形(O为圆心)铝皮上截取一块矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长AB=xm,圆柱的体积为Vm3 .
圆形(O为圆心)铝皮上截取一块矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长AB=xm,圆柱的体积为Vm3 . 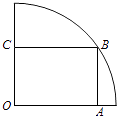
(1)写出体积V关于x的函数关系式,并指出定义域;
(2)当x为何值时,才能使做出的圆柱形罐子体积V最大?最大体积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)求函数f(x)的单调区间;
(2)设a>0,求函数f(x)在[2a,4a]上的最小值;
(3)某同学发现:总存在正实数a、b(a<b),使ab=ba , 试问:他的判断是否正确?若不正确,请说明理由;若正确,请直接写出a的取值范围(不需要解答过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数,
是奇函数,
(1)求实数a的值;
(2)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求实数k的取值范围;
(3)设关于x的方程f(4x﹣b)+f(﹣2x+1)=0有实数根,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆O外有一点P,作圆O的切线PM,M为切点,过PM的中点N,作割线NAB,交圆于A、B两点,连接PA并延长,交圆O于点C,连续PB交圆O于点D,若MC=BC. 
(1)求证:△APM∽△ABP;
(2)求证:四边形PMCD是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com