
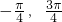 ]上单调递增,则函数g(x)的表达式为
]上单调递增,则函数g(x)的表达式为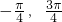 ]上都不是单调增函数,
]上都不是单调增函数, sin(x-
sin(x- ),在区间[
),在区间[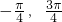 ]上单调递增,满足条件.
]上单调递增,满足条件.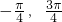 ]上没有单调性,故g(x)≠1,排除选项C.
]上没有单调性,故g(x)≠1,排除选项C. sin(x+
sin(x+ ),在区间[
),在区间[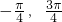 ]上没有单调性,故排除选项A.
]上没有单调性,故排除选项A. sin(x-
sin(x- ),在区间[
),在区间[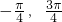 ]上单调递增,满足条件.
]上单调递增,满足条件.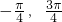 ]上没有没有单调性且在
]上没有没有单调性且在 处无意义,故排除选项D.
处无意义,故排除选项D.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com