练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知正四棱锥中，是边长为3的等边三角形，点M是的重心，过点M作与平面PAC垂直的平面，平面与截面PAC交线段的长度为2，则平面与正四棱椎表面交线所围成的封闭图形的面积可能为______________.（请将可能的结果序号填到横线上）①2；②；③3； ④.

    【答案】①③

    【解析】

    设，因为为正四棱锥，易知平面，过M作∥分别交棱、于点T、L，则平面，由题意，只需所作的平面是包含且与截面PAC交线段的长度为2即可，数形结合，作出截面即可得到答案.

    设，因为为正四棱锥，易知平面平面，又

    ，平面平面，平面，所以平面，

    过M作∥分别交棱、于点T、L，则平面，由题意，

    只需所作的平面是包含且与截面PAC交线段的长度为2即可，

    又是边长为3的等边三角形，点M是的重心，过M作∥分别交棱

    、于点E、Q，所以，即，所以，

    如图1，则平面为满足题意的平面，因为，所以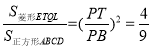，所以

    ，所以，故①正确；

    如图2，过T作∥，过L作∥，易知平面为满足题意的平面，

    且为两个全等的直角梯形，易知T、H分别为GE、EF的中点，所以，

    所以五边形的面积，

    故③正确.当∥与∥是完全相同的，所以，综上选①③.

    故答案为：①③

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】A、B两同学参加数学竞赛培训，在培训期间，他们参加了8次测验，成绩（单位：分）记录如下：

    A 71 62 72 76 63 70 85 83

    B 73 84 75 73 78 76 85

    B同学的成绩不慎被墨迹污染（，分别用m，n表示）.

    （1）用茎叶图表示这两组数据，现从A、B两同学中选派一人去参加数学竞赛，你认为选派谁更好？请说明理由（不用计算）；

    （2）若B同学的平均分为78，方差，求m，n.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在党中央的英明领导下，在全国人民的坚定支持下，中国的抗击“新型冠状肺炎”战役取得了阶段性胜利，现在摆在我们大家面前的是有序且安全的复工复产.某商场为了提振顾客的消费信心，对某中型商品实行分期付款方式销售，根据以往资料统计，顾客购买该商品选择分期付款的期数ξ的分布列为

    其中0＜a＜1，0＜b＜1.

    （1）求购买该商品的3位顾客中，恰有1位选择分4期付款的概率；

    （2）商场销售一件该商品，若顾客选择分4期付款，则商场获得的利润为2000元；若顾客选择分5期付款，则商场获得的利润为2500元；若顾客选择分6期付款，则商场获得的利润为3000元，假设该商场销售两件该商品所获得的利润为X（单位：元），

    （i）设X＝5500时的概率为m，求当m取最大值时，利润X的分布列和数学期望；

    （ii）设某数列{xn}满足x1＝0.4，xn＝a，2xn+1＝b，若a＜0.25，求n的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C：＋＝1(a>b>0)的两焦点之间的距离为2，两条准线间的距离为8，直线l：y＝k(x－m)(m∈R)与椭圆交于P，Q两点．

    (1) 求椭圆C的方程；

    (2) 设椭圆的左顶点为A，记直线AP，AQ的斜率分别为k1，k2.①若m＝0，求k1k2的值；②若k1k2＝－，求实数m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两位战士参加射击比赛训练.从若干次预赛成绩中随机抽取8次，记录如下：

    甲82 81 79 78 95 88 93 84

    乙92 95 80 75 83 80 90 85

    （1）用茎叶图表示这两组数据，并分别求两组数据的中位数；

    （2）现要从中选派一人参加射击比赛，从统计学的角度考虑，你认为选派哪位战士参加合适？请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某班级共有50名同学（男女各占一半），为弘扬传统文化，班委组织了“古诗词男女对抗赛”，将同学随机分成25组，每组男女同学各一名，每名同学均回答同样的五个不同问题，答对一题得一分，答错或不答得零分，总分5分为满分.最后25组同学得分如下表：

    组别号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    13

    男同学得分

    5

    4

    5

    5

    4

    5

    5

    4

    4

    4

    5

    5

    4

    女同学得分

    4

    3

    4

    5

    5

    5

    4

    5

    5

    5

    5

    3

    5

    分差

    1

    1

    1

    0

    -1

    0

    1

    -1

    -1

    -1

    0

    2

    -1

    组别号

    14

    15

    16

    17

    18

    19

    20

    21

    22

    23

    24

    25

    男同学得分

    4

    3

    4

    4

    4

    4

    5

    5

    5

    4

    3

    3

    女同学得分

    5

    3

    4

    5

    4

    3

    5

    5

    3

    4

    5

    5

    分差

    -1

    0

    0

    -1

    0

    1

    0

    0

    2

    0

    -2

    -2

    （I）完成列联表，并判断是否有90%的把握认为“该次对抗赛是否得满分”与“同学性别”有关；

    （Ⅱ）某课题研究小组假设各组男女同学分差服从正态分布，首先根据前20组男女同学的分差确定和，然后根据后面5组同学的分差来检验模型，检验方法是：记后面5组男女同学分差与的差的绝对值分别为，若出现下列两种情况之一，则不接受该模型，否则接受该模型.①存在；②记满足的i的个数为k，在服从正态分布的总体（个体数无穷大）中任意取5个个体，其中落在区间内的个体数大于或等于k的概率为P，.

    试问该课题研究小组是否会接受该模型.

    0.10

    0.05

    0.010

    2.706

    3.841

    6.635

    参考公式和数据：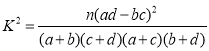

    ，；若，有，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝x2+ax+blnx（a，b∈R），曲线y＝f（x）在点（1，f（1））处的切线方程为2x﹣y﹣2＝0．

    （1）判断f（x）在定义域内的单调性，并说明理由；

    （2）若对任意的x∈（1，+∞），不等式f（x）≤m（ex﹣1﹣1）恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列的前n项和为，

    （1）求证：数列是等比数列；

    （2）若，是否存在q的某些取值，使数列中某一项能表示为另外三项之和？若能求出q的全部取值集合，若不能说明理由．

    （3）若，是否存在，使数列中，某一项可以表示为另外三项之和？若存在指出q的一个取值，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱柱中，，，.

    （1）求证：平面平面；

    （2）若，直线与平面所成角为45°，为的中点，求二面角的余弦值.

    查看答案和解析>>

    同步练习册答案