
第 届亚运会于
届亚运会于 年
年 月
月 日至
日至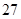 日在中国广州进行,为了做好接待工作,组委会招募了
日在中国广州进行,为了做好接待工作,组委会招募了 名男志愿者和
名男志愿者和 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有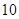 人和
人和 人喜爱运动,其余不喜爱.
人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下 列联表:
列联表:
| | 喜爱运动 | 不喜爱运动 | 总计 |
| 男 | 10 | | 16 |
| 女 | 6 | | 14 |
| 总计 | | | 30 |
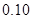 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关? 人会外语),抽取
人会外语),抽取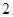 名负责翻译工作,则抽出的志愿者中
名负责翻译工作,则抽出的志愿者中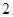 人都能胜任翻译工作的概率是多少?
人都能胜任翻译工作的概率是多少?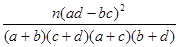
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(1) 2×2 列联表如下:
(2)在犯错的概率不超过 0.10 的前提下不能判断喜爱运动与性别有关. 喜爱运动 不喜爱运动 总计 男 10 6 16 女 6 8 14 总计 16 14 30
(3)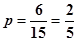 .
.
解析试题分析:(1) 2×2 列联表如下:
2分 喜爱运动 不喜爱运动 总计 男 10 6 16 女 6 8 14 总计 16 14 30
(2)假设:是否喜爱运动与性别无关,由已知数据可求得:
因此,在犯错的概率不超过 0.10 的前提下不能判断喜爱运动与性别有关. 6分
(3)喜欢运动的女志愿者有6 人,设分别为A,B,C,D,E,F,其中 A,B,C,D 会外语,则从这6 人中任取2 人有 AB,AC,AD,AE,AF,BC,BD,BE,BF,CD,CE,CF,DE,DF,EF共15 种取法, 9分
其中两人都会外语的有AB,AC,AD,BC,BD,CD 共 6 种. 11分
故抽出的志愿者中 2 人都能胜任翻译工作的概率是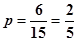 . 12分
. 12分
考点:本题考查了独立性检验的运用
点评:解决本题的步骤是,要先根据已知数据绘制列联表,然后由表格中的数据利用公式求出 的值,再由给定的数表来确定两者有关的可靠程度。
的值,再由给定的数表来确定两者有关的可靠程度。


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:解答题
7名身高互不相等的学生,分别按下列要求排列,各有多少种不同的排法?
(1)7人站成一排,要求最高的站在中间,并向左、右两边看,身高逐个递减;
(2)任取6名学生,排成二排三列,使每一列的前排学生比后排学生矮.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在对人们的休闲方式的一次调查中,共调查了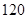 人,其中女性
人,其中女性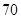 人,男性
人,男性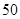 人.女性中有
人.女性中有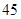 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外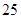 人主要的休闲方式是运动;男性中有
人主要的休闲方式是运动;男性中有 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外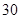 人主要的休闲方式是运动.
人主要的休闲方式是运动.
(1)根据以上数据建立一个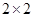 的列联表;
的列联表;
(2)判断性别与休闲方式是否有关系.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(理科)(本小题满分12分)PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,根据现行国家标准GB3095 – 2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米 ~ 75毫克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标。从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取10天的数据作为样本,监测值频数如下表所示:
| PM2.5日均值 (微克/立方米) | [25,35] | (35,45] | (45,55] | (55,65] | (65,75] | (75,85] |
| 频数 | 3 | 1 | 1 | 1 | 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(文科)某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | [230,235) | 8 | 0.16 |
| 第二组 | [235,240) | ① | 0.24 |
| 第三组 | [240,245) | 15 | ② |
| 第四组 | [245,250) | 10 | 0.20 |
| 第五组 | [250,255] | 5 | 0.10 |
| 合 计 | 50 | 1.00 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
以下茎叶图记录了甲、乙两组各四名同学的植树棵树。乙组记录中有一个数据模糊,无法确认,在图中以X表示.
(1)求甲组同学植树棵树的平均数和方差;(参考公式: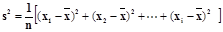 )
)
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成6组后,得到部分频率分布直方图(如图),观察图中的信息,回答下列问题.
(Ⅰ)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(Ⅱ)根据频率分布直方图,估计本次考试的平均分;
(Ⅲ)若从60名学生中随机抽取2人,抽到的学生成绩在[40,70)记0分,记[70,100]记1分,用X表示抽取结束后的总记分,求X的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
 (1)根据上表完成下面的2×2列联表(单位:人):
(1)根据上表完成下面的2×2列联表(单位:人):| | 数学成绩优秀 | 数学成绩不优秀 | 合 计 |
| 物理成绩优秀 | | | |
| 物理成绩不优秀 | | | |
| 合 计 | | | 20 |
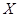 和
和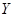 ,它们的值域分别为
,它们的值域分别为 和
和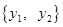 ,其样本频数列联表(称为
,其样本频数列联表(称为 列联表)为:
列联表)为:| | 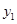 | 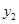 | 合计 |
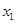 | 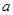 |  | 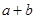 |
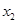 |  | 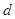 | 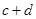 |
| 合计 | 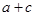 | 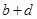 |  |
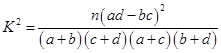 ,其中
,其中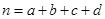 为样本容量;
为样本容量;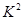 的临界值参考表:
的临界值参考表: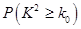 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
通过市场调查,得到某产品的资金投入x(万元)与获得的利润y(万元)的数据,如表所示:
| 资金投入x | 2 | 3 | 4 | 5 | 6 |
| 利润y | 2 | 3 | 5 | 6 | 9 |
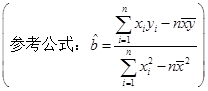
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com