
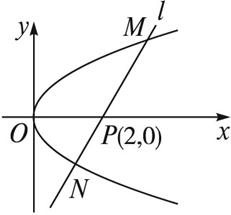
(1)写出直线l的方程;
(2)求x1x2与y1y2的值;
(3)求证:OM⊥ON.
分析:
求x1x2及y1y2,可考虑用韦达定理.证明OM⊥ON,则可用kOM·kON=-1或![]() ·
·![]() =0来证明.
=0来证明.
(1)解:直线l的方程为y=k(x-2)(k≠0). ①
(2)解:由①及y2=2x,消去y可得
k2x2-2(2k2+1)x+4k2=0. ②
点M、N的横坐标x1与x2是②的两个根,
由韦达定理,得x1x2=![]() =4.
=4.
由y12=2x1,y22=2x2,
得(y1y2)2=4x1x2=4×4=16.
由图可知y1y2<0,所以y1y2=-4.
(3)证明:设OM、ON的斜率分别为k1、k2,
则![]()
由(2)可知,y1y2=-4,x1x2=4,
所以k1k2=![]() =-1.
=-1.
所以OM⊥ON.
绿色通道:
本题的一般形式为直线l与抛物线y2=2px交于M(x1,y1)、N(x2,y2)两点,且直线l过点P(2p,0),则x1x2=4p,y1y2=-4p,OM⊥ON.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
 如图已知O为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
如图已知O为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).查看答案和解析>>
科目:高中数学 来源: 题型:
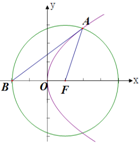 (2012•泉州模拟)如图,点O为坐标原点,直线l经过抛物线C:y2=4x的焦点F.
(2012•泉州模拟)如图,点O为坐标原点,直线l经过抛物线C:y2=4x的焦点F.| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:福建省泉州市普通中学2012届高中毕业班质量检查数学文科试题 题型:044
如图,点O为坐标原点,直线l经过抛物线C:y2=4x的焦点F.
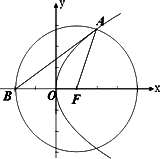
(Ⅰ)若点O到直线l的距离为![]() ,求直线l的方程;
,求直线l的方程;
(Ⅱ)设点A是直线l与抛物线C在第一象限的交点.点B是以点F为圆心,|FA|为半径的圆与x轴负半轴的交点.试判断直线AB与抛物线C的位置关系,并给出证明.
查看答案和解析>>
科目:高中数学 来源:2012年福建省泉州市高三3月质量检查数学试卷(文科)(解析版) 题型:解答题
 ,求直线l的方程;
,求直线l的方程;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com