
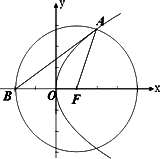
如图,点O为坐标原点,直线l经过抛物线C:y2=4x的焦点F.
(Ⅰ)若点O到直线l的距离为![]() ,求直线l的方程;
,求直线l的方程;
(Ⅱ)设点A是直线l与抛物线C在第一象限的交点.点B是以点F为圆心,|FA|为半径的圆与x轴负半轴的交点.试判断直线AB与抛物线C的位置关系,并给出证明.
解法一:(Ⅰ)抛物线的焦点![]() ,1分
,1分
当直线![]() 的斜率不存在时,即
的斜率不存在时,即![]() 不符合题意.2分
不符合题意.2分
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为:
的方程为:![]() ,即
,即![]() ;3分
;3分
所以,![]() ,解得:
,解得:![]() ;5分
;5分
故直线![]() 的方程为:
的方程为:![]() ,即
,即![]() ;6分
;6分
(Ⅱ)直线![]() 与抛物线相切,证明如下:7分
与抛物线相切,证明如下:7分
(法一):设![]() ,则
,则![]() .8分
.8分
因为![]() 所以
所以![]() ;9分
;9分
所以直线![]() 的方程为:
的方程为:![]() ,整理得:
,整理得:![]() (1)
(1)
把方程(1)代入![]() 得:
得:![]() ,10分
,10分
![]() ,
,
所以直线![]() 与抛物线相切.12分
与抛物线相切.12分
解法二:(Ⅰ)同解法一.
(Ⅱ)直线![]() 与抛物线相切,证明如下:7分
与抛物线相切,证明如下:7分
设![]() ,则
,则![]() .8分
.8分
设圆的方程为:![]() ,9分
,9分
当![]() 时,得
时,得![]() ,
,
因为点B在![]() 轴负半轴,所以
轴负半轴,所以![]() ;9分
;9分
所以直线![]() 的方程为
的方程为![]() ,整理得:
,整理得:![]() (1)
(1)
把方程(1)代入![]() 得:
得:![]() ,10分
,10分
![]() ,
,
所以直线![]() 与抛物线相切.12分
与抛物线相切.12分


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:高中数学 来源: 题型:
 如图已知O为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
如图已知O为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).查看答案和解析>>
科目:高中数学 来源: 题型:
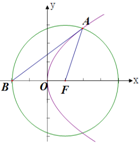 (2012•泉州模拟)如图,点O为坐标原点,直线l经过抛物线C:y2=4x的焦点F.
(2012•泉州模拟)如图,点O为坐标原点,直线l经过抛物线C:y2=4x的焦点F.| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
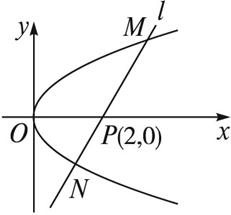
(1)写出直线l的方程;
(2)求x1x2与y1y2的值;
(3)求证:OM⊥ON.
查看答案和解析>>
科目:高中数学 来源:2012年福建省泉州市高三3月质量检查数学试卷(文科)(解析版) 题型:解答题
 ,求直线l的方程;
,求直线l的方程;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com