
已知函数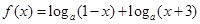 ,其中
,其中 ,记函数
,记函数 的定义域为D.
的定义域为D.
(1)求函数 的定义域D;
的定义域D;
(2)若函数 的最小值为
的最小值为 ,求
,求 的值;
的值;
(3)若对于D内的任意实数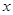 ,不等式
,不等式 <
<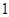 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)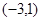
(2) 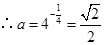
(3) (-∞, )∪[
)∪[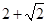 ,+∞)
,+∞)
解析试题分析:解:(1)要使函数有意义:则有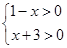 ,解得
,解得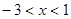
∴ 函数的定义域D为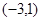 2分
2分
(2)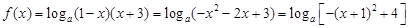
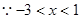
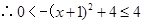
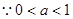 ,
,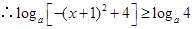 ,即
,即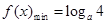 , 5分
, 5分
由 ,得
,得 ,
,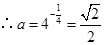 . 7分
. 7分
(注: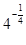 不化简为
不化简为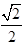 扣1分)
扣1分)
(3)由题知-x2+2mx-m2+2m<1在x∈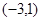 上恒成立,
上恒成立,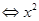 -2mx+m2-2m+1>0在x∈
-2mx+m2-2m+1>0在x∈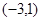 上恒成立, 8分
上恒成立, 8分
令g(x)=x2-2mx+m2-2m+1,x∈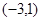 ,
,
配方得g(x)=(x-m)2-2m+1,其对称轴为x=m,
当m≤-3时, g(x)在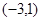 为增函数,
为增函数,
∴g(-3)= (-3-m)2-2m+1= m2+4m +10≥0,
而m2+4m +10≥0对任意实数m恒成立,∴m≤-3. 10分
②当-3<m<1时,函数g(x)在(-3,-1)为减函数,在(-1, 1)为增函数,
∴g(m)=-2m+1>0,解得m<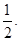 ∴-3<m<
∴-3<m< 12分
12分
③当m≥1时,函数g(x)在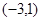 为减函数,∴g(1)= (1-m)2-2m+1= m2-4m +2≥0,
为减函数,∴g(1)= (1-m)2-2m+1= m2-4m +2≥0,
解得m≥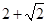 或m≤
或m≤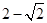 , ∴-3<m<
, ∴-3<m< 14分
14分
综上可得,实数m的取值范围是 (-∞, )∪[
)∪[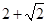 ,+∞) 16分
,+∞) 16分
考点:函数的概念和值域,二次函数的最值
点评:解决的关键是利用函数的概念以及分离参数的思想来借助于二次函数的最值得到参数的范围。属于基础题。


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
定义在R上的函数f(x)是最小正周期为2的奇函数, 且当x∈(0, 1)时, f (x)=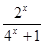 .
.
(1)求f (x)在[-1, 1]上的解析式;
(2)证明f (x)在(—1, 0)上时减函数;
(3)当λ取何值时, 不等式f (x)>λ在R上有解?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
)设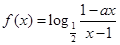 为奇函数,
为奇函数, 为常数.
为常数.
(1)求 的值;
的值;
(2)判断 在区间(1,+∞)内的单调性,并证明你的判断正确;
在区间(1,+∞)内的单调性,并证明你的判断正确;
(3)若对于区间 [3,4]上的每一个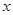 的值,不等式
的值,不等式 >
>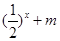 恒成立,求实数
恒成立,求实数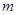 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知正比例函数y=2x的图像l1与反比例函数y= 的图像相交于点A(a,2),将直线l1向上平移3个单位得到的直线l2与双曲线相交于B、C两点(点B在第一象限),与y轴交于点D.
的图像相交于点A(a,2),将直线l1向上平移3个单位得到的直线l2与双曲线相交于B、C两点(点B在第一象限),与y轴交于点D.
(1)求反比例函数的解析式;
(2)求△DOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com