
如图,已知正比例函数y=2x的图像l1与反比例函数y= 的图像相交于点A(a,2),将直线l1向上平移3个单位得到的直线l2与双曲线相交于B、C两点(点B在第一象限),与y轴交于点D.
的图像相交于点A(a,2),将直线l1向上平移3个单位得到的直线l2与双曲线相交于B、C两点(点B在第一象限),与y轴交于点D.
(1)求反比例函数的解析式;
(2)求△DOB的面积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)是(-∞,+∞)上的增函数,a,b∈R.
(1)若a+b≥0,求证:f(a)+f(b)≥f(-a)+f(-b);
(2)判断(1)中命题的逆命题是否成立,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=x|x-a|-lnx,a∈R.
(Ⅰ)若a=1,求函数f(x)在区间[1,e]上的最大值;
(Ⅱ)若f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数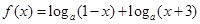 ,其中
,其中 ,记函数
,记函数 的定义域为D.
的定义域为D.
(1)求函数 的定义域D;
的定义域D;
(2)若函数 的最小值为
的最小值为 ,求
,求 的值;
的值;
(3)若对于D内的任意实数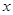 ,不等式
,不等式 <
<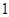 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
若函数 都在区间
都在区间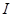 上有定义,对任意
上有定义,对任意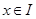 ,都有
,都有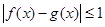 成立,则称函数
成立,则称函数 为区间
为区间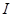 上的“伙伴函数”
上的“伙伴函数”
(1)若 为区间
为区间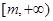 上的“伙伴函数”,求
上的“伙伴函数”,求 的范围。
的范围。
(2)判断 是否为区间
是否为区间 上的“伙伴函数”?
上的“伙伴函数”?
(3)若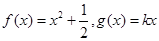 为区间
为区间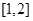 上的“伙伴函数”,求
上的“伙伴函数”,求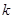 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于定义在实数集 上的两个函数
上的两个函数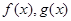 ,若存在一次函数
,若存在一次函数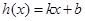 使得,对任意的
使得,对任意的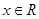 ,都有
,都有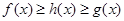 ,则把函数
,则把函数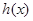 的图像叫函数
的图像叫函数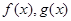 的“分界线”。现已知
的“分界线”。现已知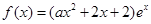 (
(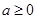 ,
,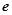 为自然对数的底数),
为自然对数的底数),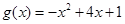
(1)求 的递增区间;
的递增区间;
(2)当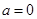 时,函数
时,函数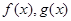 是否存在过点
是否存在过点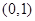 的“分界线”?若存在,求出函数
的“分界线”?若存在,求出函数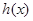 的解析式,若不存在,请说明理由。
的解析式,若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com